
| A. | y=xsinx | B. | y=$\frac{{e}^{x}+{e}^{-x}}{2}$ | C. | y=ln$\frac{1-x}{1+x}$ | D. | y=x3+x |
分析 若函數的圖象關于原點對稱,則函數為奇函數,若對任意x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$>0,則函數在[0,+∞)上為增函數;逐一分析給定四個函數的奇偶性和單調性,可得答案.
解答 解:若函數的圖象關于原點對稱,則函數為奇函數,
若對任意x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$>0,則函數在[0,+∞)上為增函數;
A中,函數y=xsinx為偶函數,不滿足條件;
B中,函數y=$\frac{{e}^{x}+{e}^{-x}}{2}$為偶函數,不滿足條件;
C中,函數y=ln$\frac{1-x}{1+x}$為奇函數,但當x≥1時,解析式無意義,不滿足條件;
D中,函數y=x3+x為奇函數,y′=3x2+1>0恒成立,故函數在[0,+∞)上為增函數,滿足條件;
故選:D
點評 本題考查的知識點是函數的奇偶性,利用導數判斷函數的單調性,正確理解題目給定的兩個條件的含義,是解答的關鍵.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1] | B. | (1,2) | C. | [1,$\sqrt{2}$) | D. | ($\sqrt{2}$,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
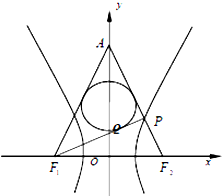 如圖,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦點分別為F1,F2,|F1F2|=2$\sqrt{3}$,P是雙曲線右支上的一點,F2P與y軸交于點A,△APF1的內切圓左邊PF1上的切點為Q,若|PQ|=1,則雙曲線的離心率是( )
如圖,已知雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦點分別為F1,F2,|F1F2|=2$\sqrt{3}$,P是雙曲線右支上的一點,F2P與y軸交于點A,△APF1的內切圓左邊PF1上的切點為Q,若|PQ|=1,則雙曲線的離心率是( )| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[\frac{5}{3},+∞)$ | B. | $(\frac{1}{5},1)$ | C. | $(1,\frac{5}{3})$ | D. | $(1,\frac{5}{3}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com