Question

1．已知橢圓C的兩個頂點分別為A（-2，0），B（2，0），焦點在x軸上，離心率為$\frac{\sqrt{3}}{2}$．
（Ⅰ）求橢圓C的方程；
（Ⅱ）點D為x軸上一點，過D作x軸的垂線交橢圓C于不同的兩點M，N，過D作AM的垂線交BN于點E．求證：△BDE與△BDN的面積之比為4：5．

Answer 1

分析 （Ⅰ）由題意設橢圓方程，由a=2，根據橢圓的離心率公式，即可求得c，則b²=a²-c²=1，即可求得橢圓的方程；
（Ⅱ）由題意分別求得DE和BN的斜率及方程，聯立即可求得E點坐標，根據三角形的相似關系，即可求得$\frac{丨BE丨}{丨BN丨}$=$\frac{4}{5}$，因此可得△BDE與△BDN的面積之比為4：5．

解答 解：（Ⅰ）由橢圓的焦點在x軸上，設橢圓方程：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0），
則a=2，e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$，則c=$\sqrt{3}$，
b²=a²-c²=1，
∴橢圓C的方程$\frac{{x}^{2}}{4}+{y}^{2}=1$；
（Ⅱ）證明：設D（x₀，0），（-2＜x₀＜2），M（x₀，y₀），N（x₀，-y₀），y₀＞0，
由M，N在橢圓上，則$\frac{{x}_{0}^{2}}{4}+{y}_{0}^{2}=1$，則x₀²=4-4y₀²，
則直線AM的斜率k_AM=$\frac{{y}_{0}-0}{{x}_{0}+2}$=$\frac{{y}_{0}}{{x}_{0}+2}$，直線DE的斜率k_DE=-$\frac{{x}_{0}+2}{{y}_{0}}$，
直線DE的方程：y=-$\frac{{x}_{0}+2}{{y}_{0}}$（x-x₀），
直線BN的斜率k_BN=$\frac{-{y}_{0}}{{x}_{0}-2}$，直線BN的方程y=$\frac{-{y}_{0}}{{x}_{0}-2}$（x-2），
$\left\{\begin{array}{l}{y=-\frac{{x}_{0}+2}{{y}_{0}}（x-{x}_{0}）}\\{y=-\frac{{y}_{0}}{{x}_{0}-2}（x-2）}\end{array}\right.$，解得：$\left\{\begin{array}{l}{x=\frac{4{x}_{0}+2}{5}}\\{y=-\frac{4}{5}{y}_{0}}\end{array}\right.$，
過E做EH⊥x軸，△BHE∽△BDN，
則丨EH丨=$\frac{4{y}_{0}}{5}$，
則$\frac{丨EH丨}{丨ND丨}$=$\frac{4}{5}$，
∴：△BDE與△BDN的面積之比為4：5．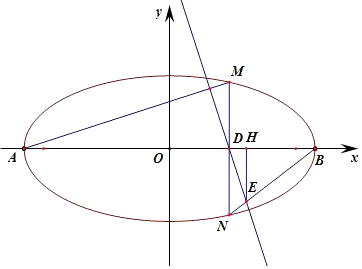

點評 本題考查橢圓的標準方程及簡單幾何性質，直線與橢圓的位置關系，直線的斜率公式，相似三角形的應用，考查數形結合思想，屬于中檔題．