
分析 (1)根據向量的平行即可得到tanx=-$\frac{\sqrt{3}}{3}$,問題得以解決,
(2)根據向量的數量積和兩角和余弦公式和余弦函數的性質即可求出
解答 解:(1)∵$\overrightarrow{a}$=(cosx,sinx),$\overrightarrow{b}$=(3,-$\sqrt{3}$),$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴-$\sqrt{3}$cosx=3sinx,
∴tanx=-$\frac{\sqrt{3}}{3}$,
∵x∈[0,π],
∴x=$\frac{5π}{6}$,
(2)f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$=3cosx-$\sqrt{3}$sinx=2$\sqrt{3}$($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)=2$\sqrt{3}$cos(x+$\frac{π}{6}$),
∵x∈[0,π],
∴x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴-1≤cos(x+$\frac{π}{6}$)≤$\frac{\sqrt{3}}{2}$,
當x=0時,f(x)有最大值,最大值3,
當x=$\frac{5π}{6}$時,f(x)有最小值,最小值-2$\sqrt{3}$.
點評 本題考查了向量的平行和向量的數量積以及三角函數的化簡和三角函數的性質,屬于基礎題


科目:高中數學 來源: 題型:選擇題
| A. | 2+i | B. | 2-i | C. | $2-\frac{1}{2}{i}$ | D. | $2+\frac{1}{2}{i}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{10}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
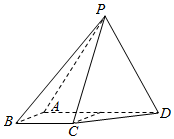 如圖,四棱錐P-ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.
如圖,四棱錐P-ABCD中,側面PAD為等邊三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
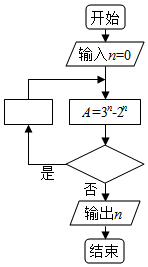 如圖程序框圖是為了求出滿足3n-2n>1000的最小偶數n,那么在
如圖程序框圖是為了求出滿足3n-2n>1000的最小偶數n,那么在 和
和 兩個空白框中,可以分別填入( )
兩個空白框中,可以分別填入( )| A. | A>1000和n=n+1 | B. | A>1000和n=n+2 | C. | A≤1000和n=n+1 | D. | A≤1000和n=n+2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com