

分析 (1)延長BC到D,過點C作CE∥BA,根據兩直線平行,同位角相等可得∠B=∠1,兩直線平行,內錯角相等可得∠A=∠2,再根據平角的定義列式整理即可得證;
(2)根據平行線的性質即可得到結論;
(3)根據平行線的性質和三角形的外角的性質即可得到結論.
解答 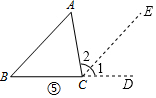 解:(1)如圖⑤,延長BC到D,過點C作CE∥BA,
解:(1)如圖⑤,延長BC到D,過點C作CE∥BA,
∵BA∥CE,
∴∠B=∠1(兩直線平行,同位角相等),
∠A=∠2(兩直線平行,內錯角相等),
又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定義),
∴∠A+∠B+∠ACB=180°(等量代換);
(2)如圖①過C作CE∥AB,
∴∠2=∠A,∠3=∠B,
∴∠ACD=∠1+∠2=∠A+∠B,
(3)如圖②,∵AB∥CD,
∴∠1=∠C,
∵∠1=∠A+∠P,
∴∠C=∠A+∠P;
如圖③,延長BA交PC于E,
∵AB∥CD,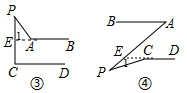
∴∠1=∠C,
∴∠1=∠C=∠BAP-∠P;
如圖④,
延長CD交AP于E,
∵AB∥CD,
∴∠A=∠AEC=∠P+(180°-∠PCD),
∴∠PCD=∠P+180°-∠A.
故答案為:∠A+∠P,∠BAP-∠P,∠P+180°-∠A.
點評 本題考查三角形外角的性質及平行線的性質,解答的關鍵是溝通外角和內角的關系.


科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
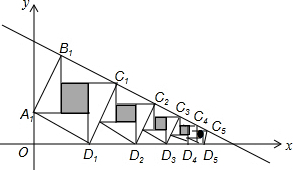 趙爽弦圖是由四個全等的直角三角形與中間的一個小正方形拼成的一個大正方形,如圖所示,若這四個全等直角三角形的兩條直角邊分別平行于x軸和y軸,大正方形的頂點B1、C1、C2、C3、…、Cn在直線y=-$\frac{1}{2}$x+$\frac{7}{2}$上,頂點D1、D2、D3、…、Dn在x軸上,則第n個陰影小正方形的面積為$({\frac{2}{3})}^{2n-2}$.
趙爽弦圖是由四個全等的直角三角形與中間的一個小正方形拼成的一個大正方形,如圖所示,若這四個全等直角三角形的兩條直角邊分別平行于x軸和y軸,大正方形的頂點B1、C1、C2、C3、…、Cn在直線y=-$\frac{1}{2}$x+$\frac{7}{2}$上,頂點D1、D2、D3、…、Dn在x軸上,則第n個陰影小正方形的面積為$({\frac{2}{3})}^{2n-2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
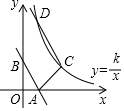 如圖,已知直線l:y=-2x+2與x軸、y軸交于A、B兩點,平移直線l交y=$\frac{k}{x}$于C、D兩點,且CD=2AB,若AC=5,求D點坐標及k的值.
如圖,已知直線l:y=-2x+2與x軸、y軸交于A、B兩點,平移直線l交y=$\frac{k}{x}$于C、D兩點,且CD=2AB,若AC=5,求D點坐標及k的值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com