
 如圖,點O是直線EP上一點,射線OA,OB,OC在直線EF的上方,射線OD在直線EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如圖,點O是直線EP上一點,射線OA,OB,OC在直線EF的上方,射線OD在直線EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.分析 (1)利用角平分線定理得到∠COD=2∠DOF=60°,再利用垂直定義得到∠BOD=90°,則∠BOC=30°,接著由OA⊥OC得到∠AOC=90°,然后利用互余計算∠AOB的度數;
(2)由角平分線定義得到∠AOB=∠AOE,再利用等角的余角相等得到∠BOC=∠COF,加上∠COF=∠DOF,于是得到∠DOF=$\frac{1}{3}$∠BOD=30°.
解答 解:(1)∵OF平分∠COD,
∴∠COD=2∠DOF=60°,
∵OB⊥OD,
∴∠BOD=90°,
∴∠BOC=90°-60°=30°,
∵OA⊥OC,
∴∠AOC=90°,
∴∠AOB=90°-30°=60°;
(2)∵OA平分∠BOE,
∴∠AOB=∠AOE,
∵OA⊥OC,
∴∠AOC=90°,
∴∠BOC=90°-∠AOB,∠COF=90°-∠AOE,
∴∠BOC=∠COF,
∵OF平分∠COD,
∴∠COF=∠DOF,
∴∠DOF=$\frac{1}{3}$∠BOD=$\frac{1}{3}$×90°=30°.
故答案為30°.
點評 本題考查了垂線:當兩條直線相交所成的四個角中,有一個角是直角時,就說這兩條直線互相垂直.也考查了角平分線的定義和鄰補角.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC中,AC=8cm,BC=6cm,AB=10cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒2cm,設運動的時間為t秒.
如圖,△ABC中,AC=8cm,BC=6cm,AB=10cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒2cm,設運動的時間為t秒.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
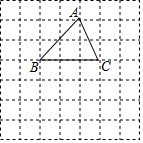 如圖,在正方形網格中,△ABC的頂點C的坐標為(2,1).
如圖,在正方形網格中,△ABC的頂點C的坐標為(2,1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com