
 如圖,△ABC中,AC=8cm,BC=6cm,AB=10cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒2cm,設運動的時間為t秒.
如圖,△ABC中,AC=8cm,BC=6cm,AB=10cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒2cm,設運動的時間為t秒.分析 (1)根據勾股定理的逆定理得到△ABC是直角三角形,當CP把△ABC的周長分成相等的兩部分時,點P在AB上,此時CA+AP=BP+BC=12cm,再根據時間=路程÷速度即可求解;
(2)根據中線的性質可知,點P在AB中點時,CP把△ABC的面積分成相等的兩部分,進而求解即可;
(3)△BCP為等腰三角形時,分三種情況進行討論:①CP=CB;②BC=BP;③PB=PC,根據等腰三角形的性質計算即可.
解答 解:(1)62+82=102,
∴△ABC是直角三角形,
由題意得,2t=10+8-2t+6,
解得,t=6,
答:當t為6時,CP把△ABC的周長分成相等的兩部分,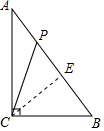
(2)∵三角形的中線把三角形的面積分成相等的兩部分,
∴2t=8+5,
解得t=6.5,
∴P經過的路程為13cm;
(3)△BCP為等腰三角形時,
分三種情況:①如果CP=CB,那么點P在AC上,CP=6cm,此時t=6÷2=3(秒);
如果CP=CB,那么點P在AB上,CP=6cm,此時t=5.4(秒);
點P還可以在AB上,作AB邊上的高CE,
$\frac{1}{2}$×AC×BC=$\frac{1}{2}$×AB×CE,
則CD=4.8,
由勾股定理得,EP=$\sqrt{{6}^{2}-4.{8}^{2}}$=3.6,
∴BP=7.2,AP=2.8,
∴t=(8+2.8)÷2=5.4(秒);
②如果BC=BP,那么點P在AB上,BP=6cm,CA+AP=8+10-6=12(cm),此時t=12÷2=6(秒);
③如果PB=PC,那么點P在BC的垂直平分線與AB的交點處,即在AB的中點,此時CA+AP=8+5=13(cm),
t=13÷2=6.5(秒);
綜上可知,當t=3秒或5.4秒或6秒或6.5秒時,△BCP為等腰三角形.
點評 本題考查的是三角形的周長、面積的計算、勾股定理的逆定理的應用,掌握三角形的中線把三角形的面積分成相等的兩部分、靈活運用分情況討論思想是解題的關鍵.


科目:初中數學 來源: 題型:解答題
 如圖,點O是直線EP上一點,射線OA,OB,OC在直線EF的上方,射線OD在直線EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如圖,點O是直線EP上一點,射線OA,OB,OC在直線EF的上方,射線OD在直線EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
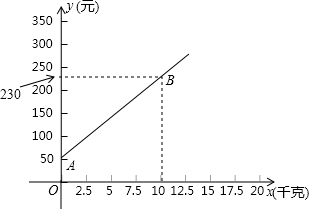 我縣甲、乙兩家甜橘柚基地生產的甜橘柚品質相同,銷售價格也相同.“元旦”期間,兩家均推出了優惠方案,甲基地的優惠方案是:每個游客進園需購買門票,采摘的甜橘柚打六折優惠;乙基地的優惠方案是:每個游客進園不需購買門票,采摘園的甜橘柚超過10千克后,超過部分打五折優惠.優惠期間,設某游客的甜橘柚采摘量為x(千克),在甲采摘園所需總費用為y1(元),在乙采摘園所需總費用為y2(元),圖中射線AB表示y1與x之間的函數關系.
我縣甲、乙兩家甜橘柚基地生產的甜橘柚品質相同,銷售價格也相同.“元旦”期間,兩家均推出了優惠方案,甲基地的優惠方案是:每個游客進園需購買門票,采摘的甜橘柚打六折優惠;乙基地的優惠方案是:每個游客進園不需購買門票,采摘園的甜橘柚超過10千克后,超過部分打五折優惠.優惠期間,設某游客的甜橘柚采摘量為x(千克),在甲采摘園所需總費用為y1(元),在乙采摘園所需總費用為y2(元),圖中射線AB表示y1與x之間的函數關系.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,正方形ABCD的頂點A的坐標為(0,3),頂點B在軸的正方向上,tan∠OBA=3,對角線AC,BD交于點P,射線OP交AB于點N,交DC于點M,點R從O出發沿OM方向以每秒$\sqrt{2}$個單位的速度運動,運動時間為t.
如圖,正方形ABCD的頂點A的坐標為(0,3),頂點B在軸的正方向上,tan∠OBA=3,對角線AC,BD交于點P,射線OP交AB于點N,交DC于點M,點R從O出發沿OM方向以每秒$\sqrt{2}$個單位的速度運動,運動時間為t.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com