
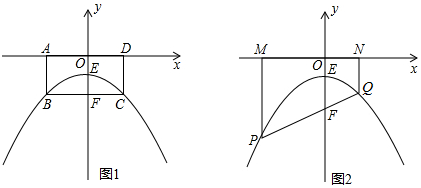
分析 (1)由題意得出拋物線頂點E(0,-1),再設頂點式根據點B坐標可得拋物線解析式;
(2)①設點P(x,-$\frac{1}{4}$x2-1),知PM=|-$\frac{1}{4}$x2-1|=$\frac{1}{4}$x2+1,根據兩點間的距離公式求得PF=$\sqrt{(0-x)^{2}+(-2+\frac{1}{4}{x}^{2}+1)^{2}}$=$\frac{1}{4}$x2+1,即可得PM=PF,同理可得QN=QF,從而得證;
②由PM+PN=PQ=m,結合S四邊形PMNQ=$\frac{\sqrt{3}}{4}$m2,即$\frac{1}{2}$(PM+PN)×MN=$\frac{\sqrt{3}}{4}$m2知MN=$\frac{\sqrt{3}}{2}$m,繼而利用勾股定理得出QH的長,即可得直線PQ的斜率k,由直線過點F(0,-2)可得答案.
解答 解:(1)由題意知點E(0,-1),
設拋物線解析式為y=ax2-1,
將點B(-2,-2)代入,得:-2=4a-1,
解得:a=-$\frac{1}{4}$,
∴y=-$\frac{1}{4}$x2-1,
則a=-$\frac{1}{4}$,b=0,c=-1,
故答案為:-$\frac{1}{4}$,0,-1;
(2)①設點P(x,-$\frac{1}{4}$x2-1),則PM=|-$\frac{1}{4}$x2-1|=$\frac{1}{4}$x2+1,
∵點F(0,-2),
∴PF=$\sqrt{(0-x)^{2}+(-2+\frac{1}{4}{x}^{2}+1)^{2}}$
=$\sqrt{{x}^{2}+\frac{1}{16}{x}^{4}-\frac{1}{2}{x}^{2}+1}$
=$\sqrt{\frac{1}{16}{x}^{4}+\frac{1}{2}{x}^{2}+1}$
=$\sqrt{(\frac{1}{4}{x}^{2}+1)^{2}}$
=$\frac{1}{4}$x2+1,
∴PM=PF,
同理可得QN=QF,
則PM+QN=PF+QF=PQ;
②由①知,PM+PN=PQ=m,
∵S四邊形PMNQ=$\frac{\sqrt{3}}{4}$m2,即$\frac{1}{2}$(PM+PN)×MN=$\frac{\sqrt{3}}{4}$m2,
∴MN=$\frac{\sqrt{3}}{2}$m,
如圖,過點P作PH⊥NQ的延長線于點H,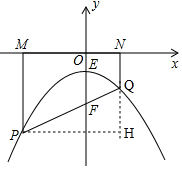
則PH=MN=$\frac{\sqrt{3}}{2}$m,
∴QH=$\sqrt{P{Q}^{2}-P{H}^{2}}$=$\sqrt{{m}^{2}-(\frac{\sqrt{3}}{2}m)^{2}}$=$\frac{m}{2}$,
∴kPQ=$\frac{QH}{PH}$=$\frac{\frac{m}{2}}{\frac{\sqrt{3}}{2}m}$=$\frac{\sqrt{3}}{3}$,
當點P在y軸右側的拋物線上時,同理可得kPQ=-$\frac{\sqrt{3}}{3}$,
又∵PQ過點F(0,-2),
∴直線PQ對應的一次函數的解析式為y-(-2)=±$\frac{\sqrt{3}}{3}$(x-0),即y=±$\frac{\sqrt{3}}{3}$x-2.
點評 本題主要考查二次函數的綜合,熟練掌握矩形的性質、待定系數法求二次函數解析式及勾股定理、兩點間的距離公式、直線的解析式是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
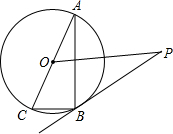 已知:如圖,AC是⊙O的直徑,BC是⊙O的弦,點P是⊙O外一點,∠PBA=∠C.
已知:如圖,AC是⊙O的直徑,BC是⊙O的弦,點P是⊙O外一點,∠PBA=∠C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com