
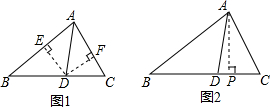
 讓我們來共同探究“三角形的角平分線”的特殊性質:
讓我們來共同探究“三角形的角平分線”的特殊性質:分析 (1)過點D作DE⊥AB,DF⊥AC,根據角平分線的性質,得出DE=DF,再根據三角形的面積計算公式,得出$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{AB}{AC}$;
(2)過點A作AP⊥BC,垂足為P,根據三角形的面積計算公式,得出$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{BD}{CD}$;
(3)根據(1)、(2)的結論,即可得出結論.
解答  解:(1)如圖1,過點D作DE⊥AB,DF⊥AC,垂足分別為E、F.
解:(1)如圖1,過點D作DE⊥AB,DF⊥AC,垂足分別為E、F.
∵AD平分∠BAC,
∴DE=DF,
又∵S△ABD=$\frac{1}{2}$×AB×DE,S△ACD=$\frac{1}{2}$×AC×DF,
∴$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{AB}{AC}$,
故答案為:DE,DF,AB,DE,AC,DF;
(2)如圖2,過點A作AP⊥BC,垂足為P,
∵S△ABD=$\frac{1}{2}$×BD×AP,S△ACD=$\frac{1}{2}$×CD×AP,
∴則$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{BD}{CD}$,
故答案為:$\frac{1}{2}$×BD×AP,$\frac{1}{2}$×CD×AP;
(3)根據(1)、(2)的結論,可得:
若在△ABC中,AD平分∠BAC,則線段AB、AC、BD、CD的關系為:$\frac{AB}{AC}$=$\frac{BD}{CD}$.
故答案為:$\frac{AB}{AC}$=$\frac{BD}{CD}$.
點評 本題主要考查了角平分線的性質以及三角形的面積的計算公式的運用,解決問題的關鍵是掌握:角的平分線上的點到角的兩邊的距離相等.解題時注意:等高的三角形的面積之比等于底邊之比.


科目:初中數學 來源: 題型:選擇題
| A. | y=$\frac{k}{x}$-1(k≠0) | B. | y=k(x-1)(k≠0) | C. | y=$\frac{k}{x-1}$(k≠0) | D. | y=$\frac{x-1}{k}$(k≠0) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某“科技創新小組”設計了一個遙控車沿直線軌道AC做勻速直線運動的模型.甲、乙兩車分別從A、B同時同向出發,沿軌道到達C處停止,甲的速度是乙的速度的2倍,設t(分)后甲、乙兩遙控車與B處的距離分別為y1(米)、y2(米),且y1、y2與t的函數關系如圖,試根據圖象解決下列問題:
某“科技創新小組”設計了一個遙控車沿直線軌道AC做勻速直線運動的模型.甲、乙兩車分別從A、B同時同向出發,沿軌道到達C處停止,甲的速度是乙的速度的2倍,設t(分)后甲、乙兩遙控車與B處的距離分別為y1(米)、y2(米),且y1、y2與t的函數關系如圖,試根據圖象解決下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
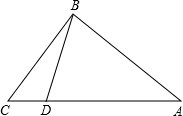 如圖,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,點D為AC邊上的動點,點D從點C出發,沿邊CA往A運動,當運動到點A時停止,設點D運動的時間為t秒,速度為每秒2個單位長度.
如圖,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,點D為AC邊上的動點,點D從點C出發,沿邊CA往A運動,當運動到點A時停止,設點D運動的時間為t秒,速度為每秒2個單位長度.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
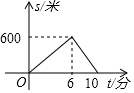 小麗、小亮從學校出發到中心書城購書,小麗步行一段時間后,小亮騎自行車沿相同路線前往,兩人均勻前行,他們的路程s(米)與小麗出發時間t(分)之間的函數關系如圖,下列說法:①小麗的速度是100米/分;②小麗出發6分鐘后小亮才出發;③學校離中心書城的路程為1000米;④小亮騎車的速度是250米/分.其中正確的是( )
小麗、小亮從學校出發到中心書城購書,小麗步行一段時間后,小亮騎自行車沿相同路線前往,兩人均勻前行,他們的路程s(米)與小麗出發時間t(分)之間的函數關系如圖,下列說法:①小麗的速度是100米/分;②小麗出發6分鐘后小亮才出發;③學校離中心書城的路程為1000米;④小亮騎車的速度是250米/分.其中正確的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
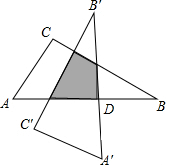 如圖,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜邊AB的中點D為旋轉中心,把這個三角形按逆時針方向旋轉90°得到Rt△A′B′C′,則旋轉后兩個直角三角形重疊部分的面積為( )
如圖,Rt△ABC中,∠C=90°,∠A=60°,AC=6,以斜邊AB的中點D為旋轉中心,把這個三角形按逆時針方向旋轉90°得到Rt△A′B′C′,則旋轉后兩個直角三角形重疊部分的面積為( )| A. | 6 | B. | 9 | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2<y3<y1 | D. | y3<y2<y1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com