

分析 根據操作步驟,可知每一次操作時所得正方形的邊長都等于原矩形的寬.所以首先需要判斷矩形相鄰的兩邊中,哪一條邊是矩形的寬.當$\frac{1}{2}$<a<1時,矩形的長為1,寬為a,所以第一次操作時所得正方形的邊長為a,剩下的矩形相鄰的兩邊分別為1-a,a.由1-a<a可知,第二次操作時所得正方形的邊長為1-a,剩下的矩形相鄰的兩邊分別為1-a,a-(1-a)=2a-1.由于(1-a)-(2a-1)=2-3a,所以(1-a)與(2a-1)的大小關系不能確定,需要分情況進行討論.又因為可以進行三次操作,故分兩種情況:①1-a>2a-1;②1-a<2a-1.對于每一種情況,分別求出操作后剩下的矩形的兩邊,根據剩下的矩形為正方形,列出方程,求出a的值.
解答 解:由題意,可知當$\frac{1}{2}$<a<1時,第一次操作后剩下的矩形的長為a,寬為1-a,所以第二次操作時正方形的邊長為1-a,第二次操作以后剩下的矩形的兩邊分別為1-a,2a-1.此時,分兩種情況:
①如果1-a>2a-1,即a<$\frac{2}{3}$,那么第三次操作時正方形的邊長為2a-1.
∵經過第三次操作后所得的矩形是正方形,
∴矩形的寬等于1-a,
即2a-1=(1-a)-(2a-1),解得a=$\frac{3}{5}$;
②如果1-a<2a-1,即a>$\frac{2}{3}$,那么第三次操作時正方形的邊長為1-a.
則1-a=(2a-1)-(1-a),解得a=$\frac{3}{4}$.
故答案為:$\frac{3}{5}$或$\frac{3}{4}$.
點評 本題考查了翻折的性質和正方形的性質以及一元一次方程的應用,解題的關鍵是分兩種情況:①1-a>2a-1;②1-a<2a-1.分別求出操作后剩下的矩形的兩邊.


科目:初中數學 來源: 題型:選擇題
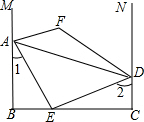 如圖,AB⊥BC,AE平分∠BAD交BC于點E,AE⊥DE,∠1+∠2=90°,M、N分別是BA、CD延長線上的點,∠EAM和∠EDN的平分線交于點F.∠F的度數為( )
如圖,AB⊥BC,AE平分∠BAD交BC于點E,AE⊥DE,∠1+∠2=90°,M、N分別是BA、CD延長線上的點,∠EAM和∠EDN的平分線交于點F.∠F的度數為( )| A. | 120° | B. | 135° | C. | 150° | D. | 不能確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 月份 | 總用電量(萬度) | 電費(萬元) |
| 7 | 12 | 6.4 |
| 8 | 16 | 8.8 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com