
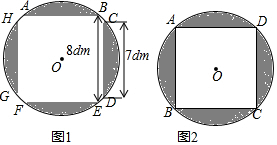
分析 (1)如圖1,過O作OM⊥CD于M,由垂徑定理得到CM=$\frac{1}{2}$CD=3.5dm,由勾股定理得到OC=$\sqrt{C{M}^{2}+O{M}^{2}}$=$\frac{\sqrt{97}}{2}$,根據圓的面積公式即可得到結論;
(2)如圖2,連接BD,由四邊形ABCD是正方形,得到∠A=90°,推出BD過圓心O,于是得到結論.
解答 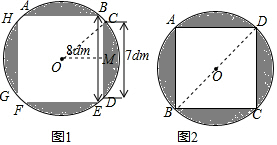 解:(1)如圖1,過O作OM⊥CD于M,
解:(1)如圖1,過O作OM⊥CD于M,
∴CM=$\frac{1}{2}$CD=3.5dm,
∵桌面上兩對邊間的距離為8dm,
∴OM=4dm,
∴OC=$\sqrt{C{M}^{2}+O{M}^{2}}$=$\frac{\sqrt{97}}{2}$,
∴桌面展開成圓形時桌面的面積=OC2•π=$\frac{97}{4}$π;
(2)如圖2,連接BD,
∵四邊形ABCD是正方形,
∴∠A=90°,
∴BD過圓心O,
∵保持原來的直徑大小不變,
∴BD=$\sqrt{97}$,
∴S正方形ABCD=$\frac{1}{2}$BD2=$\frac{97}{2}$.
點評 本題考查了正方形的性質、正方形和圓的關系,垂徑定理,圓周角定理,正確的作出輔助線是解題的關鍵.


 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:初中數學 來源: 題型:解答題
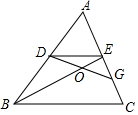 如圖,在△ABC中,點D,E分別是邊AB,AC的中點,點G是EC的中點,連接DG交BE于點O,若△ADE的面積為S,求四邊形BDGC的面積.
如圖,在△ABC中,點D,E分別是邊AB,AC的中點,點G是EC的中點,連接DG交BE于點O,若△ADE的面積為S,求四邊形BDGC的面積.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
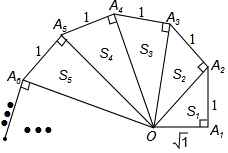 細心觀察圖形,認真分析各式,然后解答問題.
細心觀察圖形,認真分析各式,然后解答問題.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
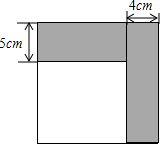 如圖所示,小明將一張正方形紙片剪去一條寬為4cm的長條后,再從剩下的長方形紙片上剪去一條寬為5cm的長條.如果兩次剪下的長條面積正好相等.
如圖所示,小明將一張正方形紙片剪去一條寬為4cm的長條后,再從剩下的長方形紙片上剪去一條寬為5cm的長條.如果兩次剪下的長條面積正好相等.查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com