
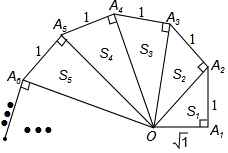
 細(xì)心觀察圖形,認(rèn)真分析各式,然后解答問題.
細(xì)心觀察圖形,認(rèn)真分析各式,然后解答問題.分析 (1)利用已知可得OAn2,注意觀察數(shù)據(jù)的變化,
(2)結(jié)合(1)中規(guī)律即可求出OA102的值即可求出,
(3)若一個(gè)三角形的面積是$\sqrt{5}$,利用前面公式可以得到它是第幾個(gè)三角形,
(4)將前10個(gè)三角形面積相加,利用數(shù)據(jù)的特殊性即可求出.
解答 解:(1)結(jié)合已知數(shù)據(jù),可得:
OAn2=n,
則Sn=$\frac{\sqrt{n}}{2}$;
(2)∵OAn2=n,
∴OA10=$\sqrt{10}$;
(3)若一個(gè)三角形的面積是$\sqrt{5}$,根據(jù):Sn=$\frac{\sqrt{n}}{2}$=$\sqrt{5}$,
則$\sqrt{n}$=2$\sqrt{5}$=$\sqrt{20}$,
則說明他是第20個(gè)三角形,
(4)S12+S22+S32+…+S102
=$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$+$\frac{4}{4}$+…+$\frac{10}{4}$
=$\frac{1+2+3+…+10}{4}$,
=$\frac{55}{4}$.
點(diǎn)評 此題主要考查了數(shù)據(jù)的規(guī)律性,綜合性較強(qiáng),關(guān)鍵是能認(rèn)真的分析總結(jié)數(shù)據(jù)的特點(diǎn).


 習(xí)題精選系列答案
習(xí)題精選系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
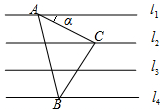 如圖,已知直線l1∥l2∥l3∥l4,相鄰兩條平行線間的距離都相等,如果等腰Rt△ABC(∠ACB=90°)的三個(gè)頂點(diǎn)分別在三條直線上,則sinα=$\frac{\sqrt{5}}{5}$.
如圖,已知直線l1∥l2∥l3∥l4,相鄰兩條平行線間的距離都相等,如果等腰Rt△ABC(∠ACB=90°)的三個(gè)頂點(diǎn)分別在三條直線上,則sinα=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
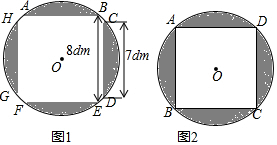
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
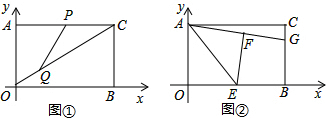
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com