
分析 (1)解方程即可解決問題.
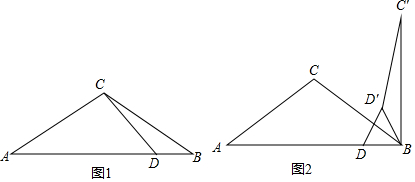
(2)如圖1中,過點C作CH⊥AB于H.在Rt△CHD中,由cos∠ADC=$\frac{\sqrt{2}}{2}$,推出∠ADC=45°,設CH=x,則DH=x,由DB=2,可得BH=x+2,在Rt△CHA中,∠A=30°,可得AH=CH÷tan30°=$\sqrt{3}$x,因為AC=BC,所以BH=AH=$\frac{1}{2}$AB,可得方程$\sqrt{3}$x=x+2,解方程即可解決問題.
(3)畫出圖形即可解決問題.
解答 解:(1)解方程x2-2x=6-3x的得到x=2或-3,
∵線段的長度為正,
∴BD=2.
(2)如圖1中,過點C作CH⊥AB于H.
在Rt△CHD中,∵cos∠ADC=$\frac{\sqrt{2}}{2}$,
∴∠ADC=45°,設CH=x,則DH=x,
∵DB=2,
∴BH=x+2,
在Rt△CHA中,∠A=30°,
∴AH=CH÷tan30°=$\sqrt{3}$x,
∵AC=BC,
∴BH=AH=$\frac{1}{2}$AB,
∴$\sqrt{3}$x=x+2,
∴x=$\sqrt{3}$+1,
∴BH=$\sqrt{3}$+3,
∴AB=2($\sqrt{3}$+3)
(3)如圖2,3中,

當α的度數為120°或240°時,易知∠BDD′=∠BD′D=∠A=∠ABC=30°,
∴△DBD′∽△ACB.
∴α的度數為120°或240°.
點評 本題考查相似形綜合題、銳角三角函數、勾股定理、相似三角形的判定和性質等知識,解題的關鍵是靈活運用所學知識解決問題,考慮問題要全面,屬于中考壓軸題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
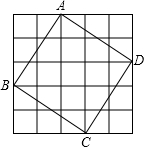 如圖,在5×5的方格中,有一個正方形ABCD,假設每一個小方格的邊長為1個單位長度,則正方形的邊長為( )
如圖,在5×5的方格中,有一個正方形ABCD,假設每一個小方格的邊長為1個單位長度,則正方形的邊長為( )| A. | $\sqrt{12}$ | B. | $\sqrt{13}$ | C. | $\sqrt{14}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y1<y2<y3 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
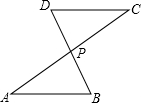 如圖,AC與BD交于點P,AP=CP,從以下四個論斷①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中選擇一個論斷作為條件,則不一定能使△APB≌△CPD的論斷是③.
如圖,AC與BD交于點P,AP=CP,從以下四個論斷①∠B=∠D,②BP=DP,③AB=CD,④AB∥CD中選擇一個論斷作為條件,則不一定能使△APB≌△CPD的論斷是③.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com