

分析 (1)連接PC,通過證明△DPC≌△EPB,得出PD=PE.
(2)分EP=EB、EP=PB、BE=BP三種情況進行解答.
解答 解:(1)PD=PE.以圖②為例,如圖,連接PC
∵△ABC是等腰直角三角形,P為斜邊AB的中點,
∴PC=PB,CP⊥AB,∠DCP=∠B=45°,
又∵∠DPC+∠CPE=90°,∠CPE+∠EPB=90°
∴∠DPC=∠EPB
在△DPC和△EPB中,
∵$\left\{\begin{array}{l}{∠DCP=∠B}\\{∠DPC=∠EPB}\\{PC=PB}\end{array}\right.$,
∴△DPC≌△EPB(ASA),
∴PD=PE;
(2)能,
①當EP=EB時,如圖1,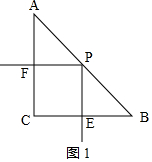
∴∠B=∠BPE=45°,
∴∠PEB=90°;
②當EP=PB時,如圖2,點E在BC上,則點E和C重合,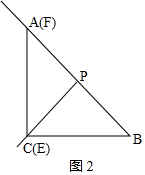
則∠PEB=∠B=45°;
③當BE=BP時,如圖3,若點E在BC上,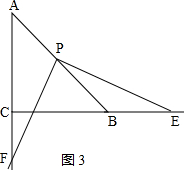
∴∠E=∠BPE,
又∵∠E+∠BPE=45°,
∴∠PEB=22.5°.
點評 本題考查了等腰三角形的性質與判定;此題是分類討論題,應分情況進行論證,不能漏解.輔助線的作出是解答本題的關鍵.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,則下列結論不成立的是( )
如圖所示,$\frac{AD}{AE}$=$\frac{AC}{AB}$=$\frac{1}{3}$,則下列結論不成立的是( )| A. | △ABE∽△ACD | B. | △BOD∽△COE | C. | OC=OD | D. | CD:BE=1:3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
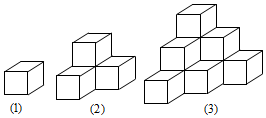 用棱長為1的小正方體按照如圖所示的擺放規律,逐個排成若干個無縫隙的幾何體,圖1幾何體表面積為6,圖2幾何體表面積為18.
用棱長為1的小正方體按照如圖所示的擺放規律,逐個排成若干個無縫隙的幾何體,圖1幾何體表面積為6,圖2幾何體表面積為18.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在6×8的網格圖中,每個小正方形邊長均為1,原點O和△ABC的頂點均為格點.
如圖,在6×8的網格圖中,每個小正方形邊長均為1,原點O和△ABC的頂點均為格點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
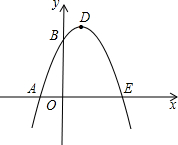 如圖,已知拋物線與x軸交于A(-1,0)、E(3,0)兩點,與y軸交于點B(0,3).
如圖,已知拋物線與x軸交于A(-1,0)、E(3,0)兩點,與y軸交于點B(0,3).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com