Question

8．如圖1，在平面直角坐標系中，△AOB為等腰直角三角形，A（4，4）

（1）求B點坐標；
（2）如圖2，若C為x軸正半軸上一動點，以AC為直角邊作等腰直角△ACD，∠ACD=90°連OD，求∠AOD的度數；
（3）如圖3，過點A作y軸的垂線交y軸于E，F為x軸負半軸上一點，G在EF的延長線上，以EG為直角邊作等腰Rt△EGH，過A作x軸垂線交EH于點M，連FM，等式AM=FM+OF是否成立？若成立，請證明：若不成立，說明理由．

Answer 1

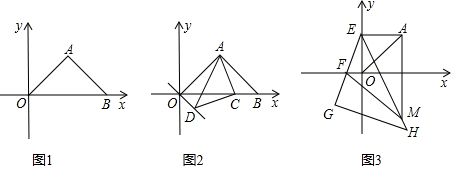
分析 （1）因為△AOB為等腰直角三角形，A（4，4），作AE⊥OB于E，則B點坐標可求；
（2）作AE⊥OB于E，DF⊥OB于F，求證△DFC≌△CEA，再根據等量變換，即可求出∠AOD的度數可求；
（3）在AM上截取AN=OF，連EN，易證△EAN≌△EOF，再根據角與角之間的關系，證明△NEM≌△FEM，則有AM-MF=OF，即可求證等式成立．

解答 解：（1）如圖所示，作AE⊥OB于E，
∵A（4，4），
∴OE=4，
∵△AOB為等腰直角三角形，且AE⊥OB，
∴OE=EB=4，
∴OB=8，
∴B（8，0）；

（2）方法一：如圖所示，作AE⊥OB于E，DF⊥OB于F，
∵△ACD為等腰直角三角形，
∴AC=DC，∠ACD=90°
即∠ACF+∠DCF=90°，
∵∠FDC+∠DCF=90°，
∴∠ACF=∠FDC，
又∵∠DFC=∠AEC=90°，
∴△DFC≌△CEA（AAS），
∴EC=DF，FC=AE，
∵A（4，4），
∴AE=OE=4，
∴FC=OE，即OF+EF=CE+EF，
∴OF=CE，
∴OF=DF，
∴∠DOF=45°，
∵△AOB為等腰直角三角形，
∴∠AOB=45°，
∴∠AOD=∠AOB+∠DOF=90°；

方法二：如圖所示，過C作CK⊥x軸交OA的延長線于K，
則△OCK為等腰直角三角形，OC=CK，∠K=45°，
又∵△ACD為等腰Rt△，
∴∠ACK=90°-∠OCA=∠DCO，AC=DC，
∴△ACK≌△DCO（SAS），
∴∠DOC=∠K=45°，
∴∠AOD=∠AOB+∠DOC=90°；

（3）AM=FM+OF成立，理由：
方法一：如圖所示，在AM上截取AN=OF，連EN．
∵A（4，4），
∴AE=OE=4，
又∵∠EAN=∠EOF=90°，AN=OF，
∴△EAN≌△EOF（SAS），
∴∠OEF=∠AEN，EF=EN，
又∵△EGH為等腰直角三角形，
∴∠GEH=45°，即∠OEF+∠OEM=45°，
∴∠AEN+∠OEM=45°
又∵∠AEO=90°，
∴∠NEM=45°=∠FEM，
又∵EM=EM，
∴△NEM≌△FEM（SAS），
∴MN=MF，
∴AM-MF=AM-MN=AN，
∴AM-MF=OF，
即AM=FM+OF；

方法二：如圖所示，在x軸的負半軸上截取ON=AM，連EN，MN，
則△EAM≌△EON（SAS），
∴EN=EM，∠NEO=∠MEA，
即∠NEF+∠FEO=∠MEA，
而∠MEA+∠MEO=90°，
∴∠NEF+∠FEO+∠MEO=90°，
而∠FEO+∠MEO=45°，
∴∠NEF=45°=∠MEF，
∴△NEF≌△MEF（SAS），
∴NF=MF，
∴AM=OF=OF+NF=OF+MF，
即AM=FM+OF．

點評 此題屬于三角形綜合題，主要考查了全等三角形的判定、等腰三角形的性質和坐標與圖形性質的綜合應用，考核了學生綜合運用數學知識的能力．解決問題的關鍵是根據截長補短的方法，作輔助線構造全等三角形，根據全等三角形的性質進行推導計算．