
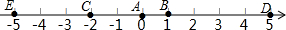 如圖,A點的初始位置位于數軸上的原點,現對A點做如下移動:第1次從原點向右移動1個單位長度至B點,第2次從B點向左移動3個單位長度至C點,第3次從C點向右移動6個單位長度至D點,第4次從D點向左移動9個單位長度至E點,…,依此類推,這樣至少移動1001次后該點到原點的距離不小于1499.
如圖,A點的初始位置位于數軸上的原點,現對A點做如下移動:第1次從原點向右移動1個單位長度至B點,第2次從B點向左移動3個單位長度至C點,第3次從C點向右移動6個單位長度至D點,第4次從D點向左移動9個單位長度至E點,…,依此類推,這樣至少移動1001次后該點到原點的距離不小于1499. 分析 利用題意得到移動1次后到原點的距離為1;移動2次后到原點的距離為2;移動3次后到原點的距離為4;移動4次后到原點的距離為5;移動5次后該點到原點的距離為7;移動6次后該點到原點的距離為8,于是可得移動(2n-1)次后該點到原點的距離為3n-2;移動2n次后該點到原點的距離為3n-1;當3n-2≥1499時,得到n最小值為501,當3n-1≥1499時,得到n最小值為500,所以至少移動1001次后該點到原點的距離不小于1499.
解答 解:由題意可得:
移動1次后該點對應的數為0+1=1,到原點的距離為1;
移動2次后該點對應的數為1-3=-2,到原點的距離為2;
移動3次后該點對應的數為-2+6=4,到原點的距離為4;
移動4次后該點對應的數為4-9=-5,到原點的距離為5;
移動5次后該點對應的數為-5+12=7,到原點的距離為7;
移動6次后該點對應的數為7-15=-8,到原點的距離為8;
…
故移動(2n-1)次后該點到原點的距離為3n-2;
移動2n次后該點到原點的距離為3n-1.
①當3n-2≥1499時,
解得:n≥500$\frac{1}{3}$,
∵n是正整數,
∴n最小值為501,此時移動了501次.
②當3n-1≥1499時,
解得:n≥500
∵n是正整數,
∴n最小值為500,此時移動了500次.
所以至少移動1001次后該點到原點的距離不小于1499.
點評 本題考查了數軸:規定了原點、正方向、單位長度的直線叫做數軸.解決本題的關鍵是得到移動(2n-1)次后該點到原點的距離為3n-2;移動2n次后該點到原點的距離為3n-1.


科目:初中數學 來源: 題型:解答題
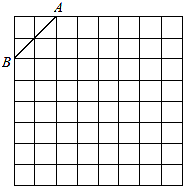 如圖是規格為8×8的正方形網格,請在所給網格中按下列要求操作:
如圖是規格為8×8的正方形網格,請在所給網格中按下列要求操作:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
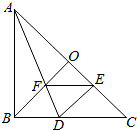 如圖,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折疊,使AB落在AC上,點B與AC上的點E重合,展開后,折痕AD交BO于點F,連接DE、EF,下列結論:①AB=2BD;②圖中有4對全等三角形;③若將△DEF沿EF折疊,則點O不一定落在AC上;④BD=BF,上述結論中正確的是( )
如圖,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折疊,使AB落在AC上,點B與AC上的點E重合,展開后,折痕AD交BO于點F,連接DE、EF,下列結論:①AB=2BD;②圖中有4對全等三角形;③若將△DEF沿EF折疊,則點O不一定落在AC上;④BD=BF,上述結論中正確的是( )| A. | ①②③④ | B. | ②④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
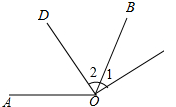 (1)已知一個角是它的余角的一半,求這個角的度數;
(1)已知一個角是它的余角的一半,求這個角的度數;查看答案和解析>>
科目:初中數學 來源: 題型:填空題
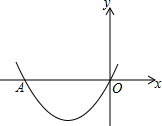 如圖,在直角坐標系xOy中,若拋物線y=$\frac{1}{2}{x^2}$+2x交x軸的負半軸于A,以O為旋轉中心,將線段OA按逆時針方向旋轉α(0°<α≤360°),再沿水平方向向右或向左平移若干個單位長度,對應線段的一個端點正好落在拋物線的頂點處,請直接寫出所有符合題意的α的值是30°或150°.
如圖,在直角坐標系xOy中,若拋物線y=$\frac{1}{2}{x^2}$+2x交x軸的負半軸于A,以O為旋轉中心,將線段OA按逆時針方向旋轉α(0°<α≤360°),再沿水平方向向右或向左平移若干個單位長度,對應線段的一個端點正好落在拋物線的頂點處,請直接寫出所有符合題意的α的值是30°或150°.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com