
分析 (1)利用配方法將已知函數方程轉化為頂點式,然后根據拋物線的性質求最值;
(2)利用配方法將已知函數方程轉化為頂點式,然后根據拋物線的性質求最值;
解答 解:(1)y=-x2-2x=-(x+1)2+1,則該拋物線的頂點坐標是(-1,1).
∵-3<x<2,該拋物線的開口方向向下,
∴當x=-1時,該函數的最大值是1;
(2)y=2x2-2x+1=2(x-$\frac{1}{2}$)2-$\frac{1}{2}$,則該拋物線的頂點坐標是($\frac{1}{2}$,-$\frac{1}{2}$).
∵-1≤x≤1,該拋物線的開口方向向上,
∴當x=$\frac{1}{2}$時,該函數的最小值是-$\frac{1}{2}$.
點評 本題考查了二次函數的最值.求二次函數的最大(小)值有三種方法,第一種可由圖象直接得出,第二種是配方法,第三種是公式法.


科目:初中數學 來源: 題型:填空題
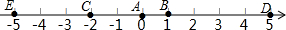 如圖,A點的初始位置位于數軸上的原點,現對A點做如下移動:第1次從原點向右移動1個單位長度至B點,第2次從B點向左移動3個單位長度至C點,第3次從C點向右移動6個單位長度至D點,第4次從D點向左移動9個單位長度至E點,…,依此類推,這樣至少移動1001次后該點到原點的距離不小于1499.
如圖,A點的初始位置位于數軸上的原點,現對A點做如下移動:第1次從原點向右移動1個單位長度至B點,第2次從B點向左移動3個單位長度至C點,第3次從C點向右移動6個單位長度至D點,第4次從D點向左移動9個單位長度至E點,…,依此類推,這樣至少移動1001次后該點到原點的距離不小于1499.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
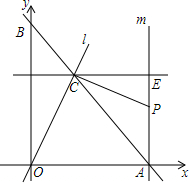 如圖,直線y=-x+$\sqrt{2}$分別交x軸、y軸于A、B兩點,經過點A的直線m⊥x軸,直線l經過原點O交線段AB于點C,過點C作OC的垂線,與直線m相交于點P,現將直線l繞O點旋轉,使交點C在線段AB上由點B向點A方向運動.
如圖,直線y=-x+$\sqrt{2}$分別交x軸、y軸于A、B兩點,經過點A的直線m⊥x軸,直線l經過原點O交線段AB于點C,過點C作OC的垂線,與直線m相交于點P,現將直線l繞O點旋轉,使交點C在線段AB上由點B向點A方向運動.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
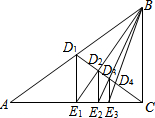 如圖,已知Rt△ABC,D1是斜邊AB的中點,過D1作D1E1⊥AC于E1,連結BE1交CD1于D2;過D2作D2E2⊥AC于E2,連結BE2交CD1于D3;過D3作D3E3⊥AC于E3,…,如此繼續,可以依次得到點D4,D5,…,Dn,分別記△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面積為S1,S2,S3,…Sn.若S△ABC=1,則S2010=$\frac{1}{201{1}^{2}}$.
如圖,已知Rt△ABC,D1是斜邊AB的中點,過D1作D1E1⊥AC于E1,連結BE1交CD1于D2;過D2作D2E2⊥AC于E2,連結BE2交CD1于D3;過D3作D3E3⊥AC于E3,…,如此繼續,可以依次得到點D4,D5,…,Dn,分別記△BD1E1,△BD2E2,△BD3E3,…,△BDnEn的面積為S1,S2,S3,…Sn.若S△ABC=1,則S2010=$\frac{1}{201{1}^{2}}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com