
 甲、乙兩人利用不同的交通工具,沿同一路線從A地出發前往B地,甲出發1h后,乙出發,兩人到達B地后立刻按原速度返回,設甲與A地相距y甲(km),乙與A地相距y乙(km),甲離開A地的時間為x(h),y甲、y乙與x之間的函數圖象如圖所示.
甲、乙兩人利用不同的交通工具,沿同一路線從A地出發前往B地,甲出發1h后,乙出發,兩人到達B地后立刻按原速度返回,設甲與A地相距y甲(km),乙與A地相距y乙(km),甲離開A地的時間為x(h),y甲、y乙與x之間的函數圖象如圖所示.分析 (1)根據題意和函數圖象即可求得甲的速度和甲從開始到返回用的時間;
(2)根據x的取值范圍不同可以求得y乙關于x的函數關系式;
(3)根據乙的函數關系式可以求得乙與A地相距240km時的時間,從而可以求得甲與A地的距離.
解答 解:(1)由題意可得,
甲的速度為:360÷6=60km/h,
甲從開始到返回A地用的時間為:6×2=12h,
故答案為:60,12;
(2)當1≤x≤5時,設y乙關于x的函數關系式是y乙=kx+b,
$\left\{\begin{array}{l}{k+b=0}\\{5k+b=360}\end{array}\right.$,得$\left\{\begin{array}{l}{k=90}\\{b=-90}\end{array}\right.$,
即當1≤x≤5時,y乙關于x的函數關系式是y乙=90x-90,
當5≤x≤9時,y乙關于x的函數關系式是y乙=mx+n,
$\left\{\begin{array}{l}{5m+n=360}\\{9m+n=0}\end{array}\right.$,得$\left\{\begin{array}{l}{m=-90}\\{n=810}\end{array}\right.$,
即當5≤x≤9時,y乙關于x的函數關系式是y乙=-90x+810,
由上可得,y乙關于x的函數關系式是y乙=$\left\{\begin{array}{l}{90x-90}&{(1≤x≤50)}\\{-90x+810}&{(5≤x≤9)}\end{array}\right.$;
(3)當y=240時,
90x-90=240,得x=$\frac{11}{3}$,
-90x+810=240,得x=$\frac{19}{3}$,
∴當x=$\frac{11}{3}$時,甲離A地的距離是:60×$\frac{11}{3}$=220(km),
當x=$\frac{19}{3}$時,甲離A地的距離是:360×2-60×$\frac{19}{3}$=340(km),
即乙與A地相距240km時,甲與A地的距離是220km或340km.
點評 本題考查一次函數的應用,解答此類問題的關鍵是明確題意,找出所求問題需要的條件,利用數形結合的思想解答.


科目:初中數學 來源: 題型:解答題
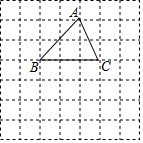 如圖,在正方形網格中,△ABC的頂點C的坐標為(2,1).
如圖,在正方形網格中,△ABC的頂點C的坐標為(2,1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
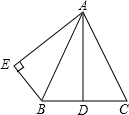 已知:如圖,AB=AC,點D是BC的中點,AD=AE,AE⊥BE,垂足為E.
已知:如圖,AB=AC,點D是BC的中點,AD=AE,AE⊥BE,垂足為E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
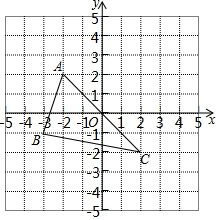 如圖,△ABC的頂點坐標分別為A(-2,2),B(-3,-1),C(2,-2).
如圖,△ABC的頂點坐標分別為A(-2,2),B(-3,-1),C(2,-2).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,線段AD、FC、EB兩兩相交,連接AB、CD、EF,則∠A+∠B+∠C+∠D+∠E+∠F=( )
如圖,線段AD、FC、EB兩兩相交,連接AB、CD、EF,則∠A+∠B+∠C+∠D+∠E+∠F=( )| A. | 360° | B. | 240° | C. | 200° | D. | 180° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com