
分析 根據(jù)解高次方程的方法可以解答此方程.
解答 解:$\left\{\begin{array}{l}{{x}^{4}+{y}^{2}+4=5yz}&{①}\\{{y}^{4}+{z}^{2}+4=5zx}&{②}\\{{z}^{4}+{x}^{2}+4=5xy}&{③}\end{array}\right.$,
通過觀察可知:x=y=z,
則將x=y=z代入①,得
x4+x2+4=5x2,
∴x4-4x2+4=0,
∴(x2-2)2=0,
得x2=2,
∴x=$±\sqrt{2}$,
∴方程組的解為:$\left\{\begin{array}{l}{x=\sqrt{2}}\\{y=\sqrt{2}}\\{z=\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{2}}\\{y=-\sqrt{2}}\\{z=-\sqrt{2}}\end{array}\right.$.
點(diǎn)評(píng) 本題考查高次方程,解答本題的關(guān)鍵是明確解高次方程的方法.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | (-3,2) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 (1)試幫助考古人員“修補(bǔ)”這個(gè)破碎的圓盤(保留作圖痕跡,并寫出作法)
(1)試幫助考古人員“修補(bǔ)”這個(gè)破碎的圓盤(保留作圖痕跡,并寫出作法)查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
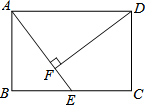 矩形ABCD中,AB=4,AD=6,點(diǎn)E是BC的中點(diǎn),過點(diǎn)D作DF⊥AE于點(diǎn)F,求cos∠ADF的值.
矩形ABCD中,AB=4,AD=6,點(diǎn)E是BC的中點(diǎn),過點(diǎn)D作DF⊥AE于點(diǎn)F,求cos∠ADF的值.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
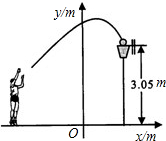 一位籃球運(yùn)動(dòng)員投籃,球沿拋物線y=-$\frac{1}{5}$x2+$\frac{7}{2}$運(yùn)行,然后準(zhǔn)確落入籃筐內(nèi),已知籃筐的中心距離底面的距離為3.05m.
一位籃球運(yùn)動(dòng)員投籃,球沿拋物線y=-$\frac{1}{5}$x2+$\frac{7}{2}$運(yùn)行,然后準(zhǔn)確落入籃筐內(nèi),已知籃筐的中心距離底面的距離為3.05m.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
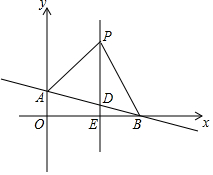 如圖,在平面直角坐標(biāo)系中,直線AB:y=kx+1(k≠0)交y軸于點(diǎn)A,交x軸于點(diǎn)B(3,0),平行于y軸的直線x=2交AB于點(diǎn)D,交x軸于點(diǎn)E,點(diǎn)P是直線x=2上一動(dòng)點(diǎn),且在點(diǎn)D的上方,設(shè)P(2,n).
如圖,在平面直角坐標(biāo)系中,直線AB:y=kx+1(k≠0)交y軸于點(diǎn)A,交x軸于點(diǎn)B(3,0),平行于y軸的直線x=2交AB于點(diǎn)D,交x軸于點(diǎn)E,點(diǎn)P是直線x=2上一動(dòng)點(diǎn),且在點(diǎn)D的上方,設(shè)P(2,n).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
 如圖,已知正方形鐵絲框ABCD邊長(zhǎng)為10,現(xiàn)使其變形為以A為圓心,AB為半徑的扇形(忽略鐵絲的粗細(xì)),則所得的扇形的面積為( )
如圖,已知正方形鐵絲框ABCD邊長(zhǎng)為10,現(xiàn)使其變形為以A為圓心,AB為半徑的扇形(忽略鐵絲的粗細(xì)),則所得的扇形的面積為( )| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com