
| A. | 1,-1 | B. | 1,-1,-2 | C. | 1,-1,-2,2 | D. | 以上均不對 |
分析 假設(x3-3x2+4x-3)(x3+2x2-x-1)=(A-B)(A+B),然后分別求出A與B的表達式,進而將原方程化為關于A、B的方程.
解答 解:設(x3-3x2+4x-3)(x3+2x2-x-1)=(A-B)(A+B),
∴$\left\{\begin{array}{l}{A+B={x}^{3}-3{x}^{2}+4x-3}\\{A-B={x}^{3}+2{x}^{2}-x-1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{A={x}^{3}-\frac{{x}^{2}}{2}+\frac{3x}{2}-1}\\{B=-\frac{5{x}^{2}}{2}+\frac{5x}{2}-1}\end{array}\right.$
∴原方程化為:(A+B)(A-B)-2B+1=0,
∴A2-(B-1)2=0
∴(A+B-1)(A-B+1)=0,
∴x3-3x2+4x-4=0或x3+2x2-x-1+1=0,
當x3-3x2+4x-4=0時,
∴(x-2)(x2-x+2)=0,
∴x=2或x2-x+2=0(無解),
當x3+2x2-x-1+1=0時,
∴x(x2+2x-1)=0,
∴x=0或x2+2x-1=0,
∴x=0或x=-1±$\sqrt{2}$
故x=0或x=2或x=-1±$\sqrt{2}$
故選(D)
點評 本題考查高次方程的解法,解題的關鍵是設(x3-3x2+4x-3)(x3+2x2-x-1)=(A-B)(A+B)進而求出A與B的表示,最后將其轉為一元二次方程來進行解答.


科目:初中數學 來源: 題型:選擇題
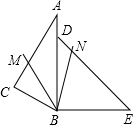 把一副三角尺ABC與BDE按如圖所示那樣拼在一起,其中A、D、B三點在同一直線上,BM為∠ABC的平分線,BN為∠CBE的平分線,則∠MBN的度數是( )
把一副三角尺ABC與BDE按如圖所示那樣拼在一起,其中A、D、B三點在同一直線上,BM為∠ABC的平分線,BN為∠CBE的平分線,則∠MBN的度數是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com