
 已知,y=-$\frac{4}{3}$x+4與x軸,y軸的交點分別是點A,B,點C(-2,3),O是原點,求點C到直線AB的距離.
已知,y=-$\frac{4}{3}$x+4與x軸,y軸的交點分別是點A,B,點C(-2,3),O是原點,求點C到直線AB的距離. 分析 根據直線解析式可以求出OA、OB的長度,即可根據勾股定理求得AB,作DC⊥AB于D,CE∥x軸,交直線AB于E,可以得出△CED∽BAO,根據相似三角形的性質即可求出點C到直線AB的距離.
解答 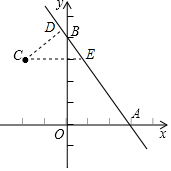 解:當x=0時,
解:當x=0時,
y=4,
當y=0時
0=-$\frac{4}{3}$x+4
x=3
∵函數y=x+4的圖象與x軸,y軸的交點分別為A、B
∴A(3,0),B(0,4)
∴OB=4,OA=3,
∵∠AOB=90°,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
作DC⊥AB于D,CE∥x軸,交直線AB于E,
∴∠CED=∠OAB,
∵點C(-2,3),
∴E點的縱坐標為3,
把y=3代入y=-$\frac{4}{3}$x+4得,3=-$\frac{4}{3}$x+4,
∴x=$\frac{3}{4}$,
∴CE=$\frac{11}{4}$,
∵∠AOB=∠EDC=90°,∠CED=∠OAB,
∴△CED∽BAO,
∴$\frac{CD}{OB}$=$\frac{CE}{AB}$,即$\frac{CD}{4}$=$\frac{\frac{11}{4}}{5}$,
∴CD=$\frac{11}{5}$
∴點C到直線AB的距離為$\frac{11}{5}$.
點評 本題考查了一次函數的圖象上點的坐標特征,勾股定理的應用,相似三角形的判定和性質,作出相似三角形是解題的關鍵.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:選擇題
| A. | a<-1 | B. | a≠0 | C. | a<1且a≠0 | D. | a<-1或a≠0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
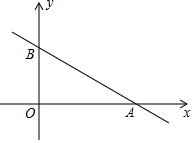 如圖,在平面直角坐標系內A(8,0),B(0,6),若直線L與AB平行,且在直線L上有且只有一點P使∠OPA=90°,求滿足條件的直線L的解析式.
如圖,在平面直角坐標系內A(8,0),B(0,6),若直線L與AB平行,且在直線L上有且只有一點P使∠OPA=90°,求滿足條件的直線L的解析式.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
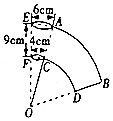 如圖所示是一個紙杯,它的母線延長后形成的立體圖形是圓錐,該圓錐的側面展開圖是扇形OAB,經測量,紙杯開口圓的直徑為6cm,下底面直徑為4cm,母線長EF=9cm,求扇形OAB的圓心角及這個紙杯的表面積.(結果保留根號和π)
如圖所示是一個紙杯,它的母線延長后形成的立體圖形是圓錐,該圓錐的側面展開圖是扇形OAB,經測量,紙杯開口圓的直徑為6cm,下底面直徑為4cm,母線長EF=9cm,求扇形OAB的圓心角及這個紙杯的表面積.(結果保留根號和π)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
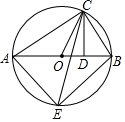 如圖,Rt△ABC內接于⊙O,∠ACB=90°,CD⊥AB于點D,CE平分∠OCD.
如圖,Rt△ABC內接于⊙O,∠ACB=90°,CD⊥AB于點D,CE平分∠OCD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1,-1 | B. | 1,-1,-2 | C. | 1,-1,-2,2 | D. | 以上均不對 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
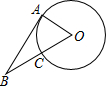 如圖,已知AB為⊙O的切線,切點為A,連接BO,BO與⊙O交于點C,若AB=2CO,則sin∠ABO的值為( )
如圖,已知AB為⊙O的切線,切點為A,連接BO,BO與⊙O交于點C,若AB=2CO,則sin∠ABO的值為( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com