
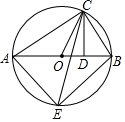
 如圖,Rt△ABC內接于⊙O,∠ACB=90°,CD⊥AB于點D,CE平分∠OCD.
如圖,Rt△ABC內接于⊙O,∠ACB=90°,CD⊥AB于點D,CE平分∠OCD.分析 (1)首先連接OE,易證得∠OCE=∠E=∠ECD,即可判定OE∥CD,又由垂徑定理,即可證得$\widehat{EA}$=$\widehat{EB}$;
(2)首先過點A作AN⊥CE于點N,作BM⊥CE于點M,易證得△AEN≌△EBM,△BCM是等腰直角三角形,繼而可得AN+BM=CE,繼而求得答案.
解答 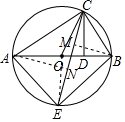 解:(1)連接OE,
解:(1)連接OE,
∵OE=OC,
∴∠OCE=∠E,
∵CE平分∠OCD交⊙O于E,
∴∠DCE=∠OCE,
∴∠DCE=∠E,
∴OE∥CD,
∵CD⊥AB,
∴OE⊥AB,
∴$\widehat{EA}$=$\widehat{EB}$,
∴EA=EB;
(2)過點A作AN⊥CE于點N,作BM⊥CE于點M,
∵AB為⊙O的直徑,
∴∠AEB=∠ACB=90°,
∴∠AEN+∠BEM=∠BEM+∠EBM=90°,
∴∠AEN=∠EMB,
∵CE平分∠OCD,
∴EA=EB,∠BCM=45°,
∴AE=BE,△BCM是等腰直角三角形,
在△AEN和△EBM中,$\left\{\begin{array}{l}{∠AEN=∠EBM}\\{∠ANB=∠EMB}\\{AE=BE}\end{array}\right.$,
∴△AEN≌△EBM(AAS),
∴AN=EM,
∴AN+BM=EM+CM=CE=4,
∴S四邊形ACBE=S△ACE+S△BCE=$\frac{1}{2}$CE•AN+$\frac{1}{2}$CE•BM=$\frac{1}{2}$CE•(AN+BM)=$\frac{1}{2}$CE•CE=$\frac{1}{2}$×4×4=8.
點評 此題考查了圓周角定理、全等三角形的判定與性質以及等腰直角三角形性質.此題難度適中,注意掌握輔助線的作法,注意掌握數形結合思想的應用.


科目:初中數學 來源: 題型:選擇題
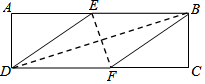 在矩形ABCD中,有一個菱形BFDE(點E,F分別在線段AB,CD上),記它們的面積分別為SABCD和SBFDE,現給出下列命題:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,則tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,則DF=2AD,則( )
在矩形ABCD中,有一個菱形BFDE(點E,F分別在線段AB,CD上),記它們的面積分別為SABCD和SBFDE,現給出下列命題:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,則tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,則DF=2AD,則( )| A. | ①是假命題,②是假命題 | B. | ①是真命題,②是假命題 | ||
| C. | ①是假命題,②是真命題 | D. | ①是真命題,②是真命題 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com