
 在2016年巴西里約奧運會上,中國女排克服重重困難,憑借頑強的毅力和超強的實力先后戰勝了實力同樣超強的巴西隊,荷蘭隊和塞爾維亞隊,獲得了奧運冠軍,為祖國和人民爭了光.
在2016年巴西里約奧運會上,中國女排克服重重困難,憑借頑強的毅力和超強的實力先后戰勝了實力同樣超強的巴西隊,荷蘭隊和塞爾維亞隊,獲得了奧運冠軍,為祖國和人民爭了光.分析 (1)利用拋物線的頂點F的坐標為(6,2.8),將點(0,2)代入解析式求出即可;
(2)利用當x=9時,y=-$\frac{1}{45}$(x-6)2+2.8=2.6,當y=0時,-$\frac{1}{45}$(x-6)2+2.8=-0.4,分別得出即可;
(3)設拋物線解析式為y=a(x-6)2+h,由點C(0,2)得解析式為y=$\frac{2-h}{36}$(x-6)2+h,再依據x=18時y≤0即可得h的范圍.
解答 解:(1)由題意可得拋物線的頂點F的坐標為(6,2.8),
設拋物線的解析式為y=a(x-6)2+2.8,
將點C(0,2)代入,得:36a+2.8=2,
解得:a=-$\frac{1}{45}$,
∴y=-$\frac{1}{45}$(x-6)2+2.8;
(2)當x=9時,y=-$\frac{1}{45}$(9-6)2+2.8=2.6>2.24,
當x=18時,y=-$\frac{1}{45}$(18-6)2+2.8=-0.4<0,
∴這次發球可以過網且不出邊界;
(3)設拋物線解析式為y=a(x-6)2+h,
將點C(0,2)代入,得:36a+h=2,即a=$\frac{2-h}{36}$,
∴此時拋物線解析式為y=$\frac{2-h}{36}$(x-6)2+h,
根據題意,得:$\frac{144(2-h)}{36}$+h≤0,
解得:h≥$\frac{8}{3}$,
又∵h>2.32,
∴h≥$\frac{8}{3}$
答:球既能過網又不會出界的h的取值范圍是h≥$\frac{8}{3}$.
點評 此題主要考查了二次函數的應用題,求范圍的問題,可以利用臨界點法求出自變量的值,再根據題意確定范圍.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案 名校聯盟快樂課堂系列答案
名校聯盟快樂課堂系列答案科目:初中數學 來源: 題型:解答題
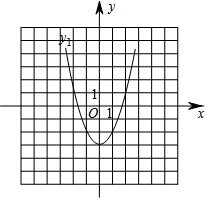 如圖為拋物線y1=x2-3,且拋物線y2是由拋物線y1向右平移2個單位得到的.
如圖為拋物線y1=x2-3,且拋物線y2是由拋物線y1向右平移2個單位得到的.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC的三個頂點的坐標分別是A(-2,-4),B(0,-4),C(1,-1).
如圖,△ABC的三個頂點的坐標分別是A(-2,-4),B(0,-4),C(1,-1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com