
分析 (1)根據(jù)自變量與函數(shù)值的對應關(guān)系,可得A,B的值,根據(jù)頂點式,可得函數(shù)解析式;
(2)根據(jù)函數(shù)圖象上的點滿足函數(shù)解析式,可得N點坐標,根據(jù)勾股定理,可得答案;
(3)根據(jù)相似三角形的性質(zhì),可得關(guān)于m的方程,可得M點的坐標,要分類討論,以防遺漏.
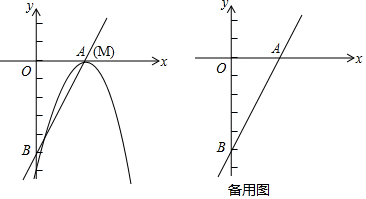
解答 解:(1)∵直線y=2x-5與x軸和y軸分別交于點A和點B,
∴A($\frac{5}{2}$,0),B(0,-5).
當點M與點A重合時,∴M($\frac{5}{2}$,0),
∴拋物線的解析式為y=-(x-$\frac{5}{2}$)2,即y=-x2+5x-$\frac{25}{4}$;
(2)N在直線y=2x-5上,設N(a,2a-5),又N在拋物線上,
∴2a-5=-a2+5a-$\frac{25}{4}$,解得a1=$\frac{1}{2}$,a2=$\frac{5}{2}$(舍去),
∴N($\frac{1}{2}$,-4).
過點N作NC⊥x軸,垂足為C,如圖1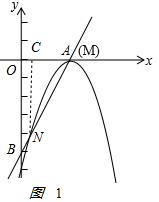 ,
,
∵N($\frac{1}{2}$,-4),
∴C($\frac{1}{2}$,0),
∴NC=4.MC=OM-OC=$\frac{5}{2}$-$\frac{1}{2}$=2,
∴MN=$\sqrt{N{C}^{2}+M{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
(3)設M(m,2m-5),N(n,2n-5).
∵A($\frac{5}{2}$,0),B(0-,5),
∴OA=$\frac{5}{2}$,OB=5,則OB=2OA,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\frac{5\sqrt{5}}{2}$,
如圖2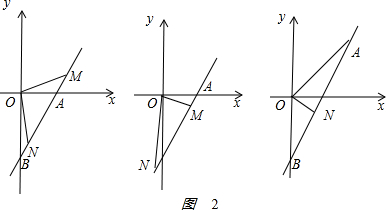 ,
,
當∠MON=90°時,∵AB≠MN,且MN和AB邊上的高相等,因此△OMN與△AOB不能全等,
∴△OMN與△AOB不相似,不滿足題意;
當∠OMN=90°時,$\frac{OA}{OB}$=$\frac{OM}{MN}$,即$\frac{1}{2}$=$\frac{OM}{2\sqrt{5}}$,解得OM=$\sqrt{5}$,
則m2+(2m-5)2=($\sqrt{5}$)2,解得m=2,∴M(2,-1);
當∠ONM=90°時,$\frac{OA}{OB}$=$\frac{ON}{MN}$,即$\frac{1}{2}$=$\frac{ON}{MN}$,解得ON=$\sqrt{5}$,則n2+(2n-5)2=($\sqrt{5}$)2,解得n=2,
∵OM2=ON2+MN2,即m2+(2m-5)2=5+(2$\sqrt{5}$)2,解得m=4,則M點的坐標為(4,3),
綜上所述:M點的坐標為(2,-1)或(4,3).
點評 本題考查了二次函數(shù)綜合題,解(1)的關(guān)鍵是頂點是函數(shù)解析式;解(2)的關(guān)鍵是利用函數(shù)圖象上的點滿足函數(shù)解析式得出N點坐標;解(3)的關(guān)鍵是利用相似三角形的性質(zhì)得出關(guān)于m的方程,要分類討論,以防遺漏.


科目:初中數(shù)學 來源: 題型:解答題
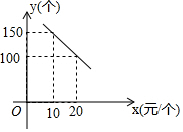 某旅游風景區(qū)出售一種紀念品,該紀念品的成本為12元/個,這種紀念品的銷售價格為x(元/個)與每天的銷售數(shù)量y(個)之間的函數(shù)關(guān)系如圖所示.
某旅游風景區(qū)出售一種紀念品,該紀念品的成本為12元/個,這種紀念品的銷售價格為x(元/個)與每天的銷售數(shù)量y(個)之間的函數(shù)關(guān)系如圖所示.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 在2016年巴西里約奧運會上,中國女排克服重重困難,憑借頑強的毅力和超強的實力先后戰(zhàn)勝了實力同樣超強的巴西隊,荷蘭隊和塞爾維亞隊,獲得了奧運冠軍,為祖國和人民爭了光.
在2016年巴西里約奧運會上,中國女排克服重重困難,憑借頑強的毅力和超強的實力先后戰(zhàn)勝了實力同樣超強的巴西隊,荷蘭隊和塞爾維亞隊,獲得了奧運冠軍,為祖國和人民爭了光.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 某商場為了吸引顧客,設立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤(如圖,轉(zhuǎn)盤被平均分成20份),并規(guī)定:顧客每購物滿200元,就能獲得一次轉(zhuǎn)動轉(zhuǎn)盤的機會.如果轉(zhuǎn)盤停止后,指針正好對準紅色、黃色、綠色區(qū)域,那么顧客就可以分別獲得50元、30元、20元的購物券,憑購物券可以在該商場繼續(xù)購物.如果顧客不愿意轉(zhuǎn)盤,那么可直接獲得10元的購物券.
某商場為了吸引顧客,設立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤(如圖,轉(zhuǎn)盤被平均分成20份),并規(guī)定:顧客每購物滿200元,就能獲得一次轉(zhuǎn)動轉(zhuǎn)盤的機會.如果轉(zhuǎn)盤停止后,指針正好對準紅色、黃色、綠色區(qū)域,那么顧客就可以分別獲得50元、30元、20元的購物券,憑購物券可以在該商場繼續(xù)購物.如果顧客不愿意轉(zhuǎn)盤,那么可直接獲得10元的購物券.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
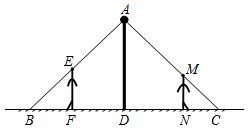 如圖,小強和小華共同站在路燈下,小強的身高EF=1.8m,小華的身高MN=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m.
如圖,小強和小華共同站在路燈下,小強的身高EF=1.8m,小華的身高MN=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com