
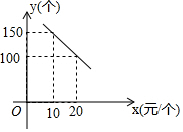
 某旅游風景區出售一種紀念品,該紀念品的成本為12元/個,這種紀念品的銷售價格為x(元/個)與每天的銷售數量y(個)之間的函數關系如圖所示.
某旅游風景區出售一種紀念品,該紀念品的成本為12元/個,這種紀念品的銷售價格為x(元/個)與每天的銷售數量y(個)之間的函數關系如圖所示.分析 (1)根據函數圖象中兩個點的坐標,利用待定系數法求解可得;
(2)根據“總利潤=單件利潤×銷售量”列出函數解析,利用二次函數的性質可得最值情況;
(3)根據(2)中相等關系列出函數解析式,由二次函數的性質求解可得.
解答 解:(1)設y=kx+b,
根據函數圖象可得:$\left\{\begin{array}{l}{10k+b=150}\\{20k+b=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-5}\\{b=200}\end{array}\right.$,
∴y=-5x+200;
(2)設每天獲利w元,
則w=(x-12)y=-5x2+260x-2400=-5(x-26)2+980,
∴當x=26時,w最大,最大利潤為980元;
(3)設“十一”假期每天利潤為P元,
則P=(0.8x-12)•y(1+200%)=-12x2+660x-7200=-12(x-$\frac{55}{2}$)2+1875,
∴當x=$\frac{55}{2}$時,P最大,
此時售價為0.8×$\frac{55}{2}$=22,
答:“十•一”假期該紀念品打八折后售價為22元.
點評 本題主要考查二次函數的應用和待定系數法求一次函數的解析式,熟練掌握銷售問題中關于總利潤的相等關系和二次函數的性質是解題的關鍵.


科目:初中數學 來源: 題型:解答題
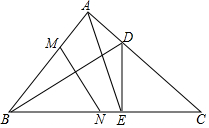 如圖,△ABC中,∠BAC=90°,AB=AC,D為AC上一點,DE⊥BC于E,連接BD,M在AB上,AM=AD,MN⊥BD交BC于點N,若MN=5,AE=5$\sqrt{2}$,求BC的長.
如圖,△ABC中,∠BAC=90°,AB=AC,D為AC上一點,DE⊥BC于E,連接BD,M在AB上,AM=AD,MN⊥BD交BC于點N,若MN=5,AE=5$\sqrt{2}$,求BC的長.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | -2$\frac{3}{5}$ | D. | -$\frac{5}{13}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,△ABC的三個頂點的坐標分別是A(-2,-4),B(0,-4),C(1,-1).
如圖,△ABC的三個頂點的坐標分別是A(-2,-4),B(0,-4),C(1,-1).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖.在正方形ABCD中,點P是BC延長線上一點,BQ⊥PD于點Q,QN⊥BD于點N,連接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,則AN的長為$\sqrt{10}$.
如圖.在正方形ABCD中,點P是BC延長線上一點,BQ⊥PD于點Q,QN⊥BD于點N,連接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,則AN的長為$\sqrt{10}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com