
 如圖.在正方形ABCD中,點(diǎn)P是BC延長線上一點(diǎn),BQ⊥PD于點(diǎn)Q,QN⊥BD于點(diǎn)N,連接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,則AN的長為$\sqrt{10}$.
如圖.在正方形ABCD中,點(diǎn)P是BC延長線上一點(diǎn),BQ⊥PD于點(diǎn)Q,QN⊥BD于點(diǎn)N,連接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,則AN的長為$\sqrt{10}$. 分析 設(shè)NQ與CD交于點(diǎn)O,作QH⊥CD于H,NG⊥AD于G.由$\frac{1}{2}$•DM•QH=$\frac{1}{8}$DM2,推出QH=$\frac{1}{4}$DM,設(shè)HQ=a,則DM=4a,由BQ⊥PD,推出△DHQ∽△QHM,設(shè)DH=x,則MH=4a-x,可得HQ2=DH•HM,推出a2=x(4a-x),解得x=(2+$\sqrt{3}$)a,由tan∠CDP=$\frac{HQ}{DH}$=$\frac{CP}{CD}$,可得$\frac{a}{(2+\sqrt{3})a}$=$\frac{CP}{4}$,推出CP=4(2-$\sqrt{3}$),由△BCM≌△DCP,由此CM=CP=4(2-$\sqrt{3}$),推出DM=DC-CM=4-4(2-$\sqrt{3}$)=4$\sqrt{3}$-4,由4a=4$\sqrt{3}$-4,推出a=$\sqrt{3}$-1,由HQ∥PC,推出$\frac{HQ}{PC}$=$\frac{DH}{DC}$,可得$\frac{\sqrt{3}-1}{4(2-\sqrt{3})}$=$\frac{DH}{4}$,推出DH=$\sqrt{3}$+1,推出DQ=$\sqrt{D{H}^{2}+H{Q}^{2}}$=2$\sqrt{2}$,由 QN⊥BD,易知△DQN∽△DBQ,可得DQ2=DN•DB,可得DN=$\frac{(2\sqrt{2})^{2}}{4\sqrt{2}}$=$\sqrt{2}$,由此即解決問題.
解答 解:設(shè)NQ與CD交于點(diǎn)O,作QH⊥CD于H,NG⊥AD于G.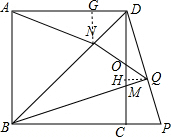
∵$\frac{1}{2}$•DM•QH=$\frac{1}{8}$DM2,
∴QH=$\frac{1}{4}$DM,設(shè)HQ=a,則DM=4a,
∵BQ⊥PD,
由△DHQ∽△QHM,設(shè)DH=x,則MH=4a-x,
可得HQ2=DH•HM,
∴a2=x(4a-x),
解得x=(2+$\sqrt{3}$)a,
∴tan∠CDP=$\frac{HQ}{DH}$=$\frac{CP}{CD}$,
∴$\frac{a}{(2+\sqrt{3})a}$=$\frac{CP}{4}$,
∴CP=4(2-$\sqrt{3}$),
易證△BCM≌△DCP,
∴CM=CP=4(2-$\sqrt{3}$),
∴DM=DC-CM=4-4(2-$\sqrt{3}$)=4$\sqrt{3}$-4,
∴4a=4$\sqrt{3}$-4,
∴a=$\sqrt{3}$-1,
∵HQ∥PC,
∴$\frac{HQ}{PC}$=$\frac{DH}{DC}$,
∴$\frac{\sqrt{3}-1}{4(2-\sqrt{3})}$=$\frac{DH}{4}$,
∴DH=$\sqrt{3}$+1,
∴DQ=$\sqrt{D{H}^{2}+H{Q}^{2}}$=2$\sqrt{2}$,
∵QN⊥BD,易知△DQN∽△DBQ,可得DQ2=DN•DB,
∴DN=$\frac{(2\sqrt{2})^{2}}{4\sqrt{2}}$=$\sqrt{2}$,
∵∠GDN=45°,
∴GN=DG=1,
在Rt△AGN中,AG=3,GN=1,
∴AN=$\sqrt{A{G}^{2}+G{N}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
故答案為$\sqrt{10}$.
點(diǎn)評 本題考查正方形的性質(zhì)、相似三角形的判定和性質(zhì)、全等三角形的判定和性質(zhì)、勾股定理,三角形的面積等知識,解題的關(guān)鍵是學(xué)會添加常用輔助線,構(gòu)造直角三角形解決問題,屬于中考填空題中的壓軸題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
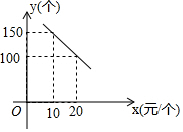 某旅游風(fēng)景區(qū)出售一種紀(jì)念品,該紀(jì)念品的成本為12元/個,這種紀(jì)念品的銷售價格為x(元/個)與每天的銷售數(shù)量y(個)之間的函數(shù)關(guān)系如圖所示.
某旅游風(fēng)景區(qū)出售一種紀(jì)念品,該紀(jì)念品的成本為12元/個,這種紀(jì)念品的銷售價格為x(元/個)與每天的銷售數(shù)量y(個)之間的函數(shù)關(guān)系如圖所示.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 某商場為了吸引顧客,設(shè)立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤(如圖,轉(zhuǎn)盤被平均分成20份),并規(guī)定:顧客每購物滿200元,就能獲得一次轉(zhuǎn)動轉(zhuǎn)盤的機(jī)會.如果轉(zhuǎn)盤停止后,指針正好對準(zhǔn)紅色、黃色、綠色區(qū)域,那么顧客就可以分別獲得50元、30元、20元的購物券,憑購物券可以在該商場繼續(xù)購物.如果顧客不愿意轉(zhuǎn)盤,那么可直接獲得10元的購物券.
某商場為了吸引顧客,設(shè)立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤(如圖,轉(zhuǎn)盤被平均分成20份),并規(guī)定:顧客每購物滿200元,就能獲得一次轉(zhuǎn)動轉(zhuǎn)盤的機(jī)會.如果轉(zhuǎn)盤停止后,指針正好對準(zhǔn)紅色、黃色、綠色區(qū)域,那么顧客就可以分別獲得50元、30元、20元的購物券,憑購物券可以在該商場繼續(xù)購物.如果顧客不愿意轉(zhuǎn)盤,那么可直接獲得10元的購物券.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
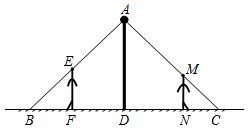 如圖,小強(qiáng)和小華共同站在路燈下,小強(qiáng)的身高EF=1.8m,小華的身高M(jìn)N=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m.
如圖,小強(qiáng)和小華共同站在路燈下,小強(qiáng)的身高EF=1.8m,小華的身高M(jìn)N=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,一長梯靠在墻上,當(dāng)梯子底端距離墻腳5米時,梯子的頂端高出地面9米;現(xiàn)梯子的頂端向上移動1米,求此時梯子的底端與墻腳的距離.
如圖,一長梯靠在墻上,當(dāng)梯子底端距離墻腳5米時,梯子的頂端高出地面9米;現(xiàn)梯子的頂端向上移動1米,求此時梯子的底端與墻腳的距離.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
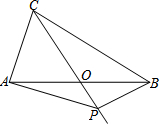 如圖,在△ABC中,AB=BC=6,AO=BO,P是射線CO上的一個動點(diǎn),∠AOC=60°,則當(dāng)△PAB為直角三角形時,sin∠PAB=$\frac{1}{2}$或$\frac{\sqrt{21}}{7}$或$\frac{\sqrt{3}}{2}$.
如圖,在△ABC中,AB=BC=6,AO=BO,P是射線CO上的一個動點(diǎn),∠AOC=60°,則當(dāng)△PAB為直角三角形時,sin∠PAB=$\frac{1}{2}$或$\frac{\sqrt{21}}{7}$或$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com