
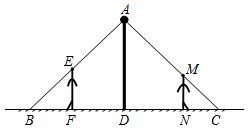
 如圖,小強和小華共同站在路燈下,小強的身高EF=1.8m,小華的身高MN=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m.
如圖,小強和小華共同站在路燈下,小強的身高EF=1.8m,小華的身高MN=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m. 分析 設路燈的高度為xm,根據相似三角形對應邊成比例可得,$\frac{EF}{AD}$=$\frac{BF}{BD}$,即$\frac{1.8}{x}$=$\frac{1.8}{1.8+DF}$,可得DF的表達式,再根據相似三角形對應邊成比例,同樣可得DN的表達式,由于DF+DN=4.7,可得關于x的方程,然后解方程求出x即可.
解答  解:設路燈的高度為xm,
解:設路燈的高度為xm,
∵EF∥AD,
∴△BEF∽△BAD,
∴$\frac{EF}{AD}$=$\frac{BF}{BD}$,
即$\frac{1.8}{x}$=$\frac{1.8}{1.8+DF}$,
解得DF=x-1.8,
∵MN∥AD,
∴△CMN∽△CAD,
∴$\frac{MN}{AD}$=$\frac{CN}{CD}$,
即$\frac{1.5}{x}$=$\frac{1.5}{1.5+DN}$,
解得DN=x-1.5,
∵兩人相距4.7m,
∴FD+ND=4.7,
∴x-1.8+x-1.5=4.7,
解得x=4,
故答案為:4m.
點評 本題主要考查了相似三角形的應用以及中心投影,解決問題的關鍵是掌握:相似三角形的對應邊成比例,根據等量關系列出關于x的方程進行求解.解題時注意方程思想的運用.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖.在正方形ABCD中,點P是BC延長線上一點,BQ⊥PD于點Q,QN⊥BD于點N,連接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,則AN的長為$\sqrt{10}$.
如圖.在正方形ABCD中,點P是BC延長線上一點,BQ⊥PD于點Q,QN⊥BD于點N,連接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,則AN的長為$\sqrt{10}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com