

分析 (1)根據(jù)平行四邊形的性質(zhì)可證AB∥CD,AB=CD,又由已知可證BE=DF,即證四邊形BEDF是平行四邊形,故DE=BF;
(2)連接OD,構(gòu)造直角三角形,利用OA=OD,可求得∠ODA=35°,從而根據(jù)∠CDA=∠CDO+∠ODA計算求解.
解答 (1)證明:∵四邊形ABCD是?ABCD,
∴AB∥CD,AB=CD,
∵AE=CF,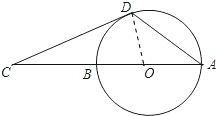
∴BE=DF,
∴四邊形BEDF是平行四邊形,
∴DE=BF;
(2)解:連接OD,則∠ODC=90°,∠COD=70°;
∵OA=OD,
∴∠ODA=∠A=$\frac{1}{2}$∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°.
點評 本題考查了平行四邊形的判定和性質(zhì),切線的性質(zhì),三角形的外角與內(nèi)角的關(guān)系,等邊對等角求解.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案科目:初中數(shù)學 來源: 題型:解答題
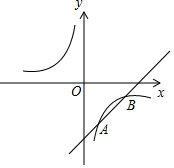 如圖,已知一次函數(shù)y=kx+b與反比例函數(shù)y=$\frac{m}{x}$交于A(1,-3),B(a,-1)兩點.
如圖,已知一次函數(shù)y=kx+b與反比例函數(shù)y=$\frac{m}{x}$交于A(1,-3),B(a,-1)兩點.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 在2016年巴西里約奧運會上,中國女排克服重重困難,憑借頑強的毅力和超強的實力先后戰(zhàn)勝了實力同樣超強的巴西隊,荷蘭隊和塞爾維亞隊,獲得了奧運冠軍,為祖國和人民爭了光.
在2016年巴西里約奧運會上,中國女排克服重重困難,憑借頑強的毅力和超強的實力先后戰(zhàn)勝了實力同樣超強的巴西隊,荷蘭隊和塞爾維亞隊,獲得了奧運冠軍,為祖國和人民爭了光.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 某商場為了吸引顧客,設(shè)立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤(如圖,轉(zhuǎn)盤被平均分成20份),并規(guī)定:顧客每購物滿200元,就能獲得一次轉(zhuǎn)動轉(zhuǎn)盤的機會.如果轉(zhuǎn)盤停止后,指針正好對準紅色、黃色、綠色區(qū)域,那么顧客就可以分別獲得50元、30元、20元的購物券,憑購物券可以在該商場繼續(xù)購物.如果顧客不愿意轉(zhuǎn)盤,那么可直接獲得10元的購物券.
某商場為了吸引顧客,設(shè)立了一個可以自由轉(zhuǎn)動的轉(zhuǎn)盤(如圖,轉(zhuǎn)盤被平均分成20份),并規(guī)定:顧客每購物滿200元,就能獲得一次轉(zhuǎn)動轉(zhuǎn)盤的機會.如果轉(zhuǎn)盤停止后,指針正好對準紅色、黃色、綠色區(qū)域,那么顧客就可以分別獲得50元、30元、20元的購物券,憑購物券可以在該商場繼續(xù)購物.如果顧客不愿意轉(zhuǎn)盤,那么可直接獲得10元的購物券.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
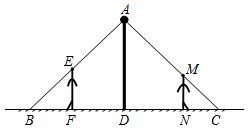 如圖,小強和小華共同站在路燈下,小強的身高EF=1.8m,小華的身高MN=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m.
如圖,小強和小華共同站在路燈下,小強的身高EF=1.8m,小華的身高MN=1.5m,他們的影子恰巧等于自己的身高,即BF=1.8m,CN=1.5m,且兩人相距4.7m,則路燈AD的高度是4m.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
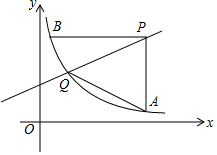 如圖,直線y=$\frac{1}{2}$x+m與反比例函數(shù)y=$\frac{k}{x}$(x>0)的圖象交于Q點,點B(1,6)在反比例函數(shù)的圖象上,過B作BP∥x軸交直線y=$\frac{1}{2}$x+m于點P,過點P作PA∥y軸交雙曲線于點A,連結(jié)AQ,BQ.
如圖,直線y=$\frac{1}{2}$x+m與反比例函數(shù)y=$\frac{k}{x}$(x>0)的圖象交于Q點,點B(1,6)在反比例函數(shù)的圖象上,過B作BP∥x軸交直線y=$\frac{1}{2}$x+m于點P,過點P作PA∥y軸交雙曲線于點A,連結(jié)AQ,BQ.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com