
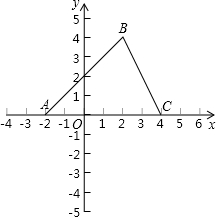
 如圖,在直角坐標系中,△ABC的頂點A(-2,0),B(2,4),C(4,0).
如圖,在直角坐標系中,△ABC的頂點A(-2,0),B(2,4),C(4,0).分析 (1)利用三角形的面積公式計算即可;
(2)設出點D坐標,進而得出點E坐標,表示出AE,CE,最后用三角形的面積公式建立方程求解即可;
(3)由平行四邊形的性質即可得出結論;
(4)平行四邊形的面積等于一條對角線將它分成的兩個三角形中一個的2倍即可.
解答 解:(1)如圖1,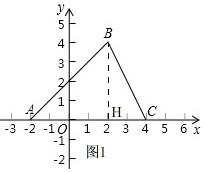 過點B作BH⊥AC于D,
過點B作BH⊥AC于D,
∵A(-2,0),B(2,4),C(4,0),
∴AC=6,BH=4,
∴S△ABC=$\frac{1}{2}$AC×BH=$\frac{1}{2}$×6×4=12,
(2)如圖2,設D(0,b),
∵B(2,4),
∴直線BD的解析式為y=$\frac{4-b}{2}$x+b,
∴E($\frac{2b}{b-4}$,0),
∴AE=$\frac{2b}{b-4}$+2,CE=4-$\frac{2b}{b-4}$,
∴S△ADE=$\frac{1}{2}$AE×OD=$\frac{1}{2}$($\frac{2b}{b-4}$+2)×(-b),
S△BCE=$\frac{1}{2}$CE×|yB|=$\frac{1}{2}$(4-$\frac{2b}{b-4}$)×4,
∵S△ADE=S△BCE,
∴$\frac{1}{2}$($\frac{2b}{b-4}$+2)×(-b)=$\frac{1}{2}$(4-$\frac{2b}{b-4}$)×4,
∴b=4(舍)或b=-4,
∴D(0,-4);
(3)答案不唯一,
理由:如圖3,
Ⅰ、以AC為邊時,過點B作BP1∥AC,
∵B(2,4),
∴直線BP1的解析式為y=4,
∵BP1∥AC,BP1=BP2=AC=6,
∴P1(8,4),P2(-4,4),
Ⅱ、當AC為對角線時,BP3與AC互相平分,
設P3(m,n),
∴m+2=2,n+4=0,
∴m=0,n=-4,
∴P3(0,-4),
即:滿足條件的點P(-4,4),(0,-4),(8,4);
(4)由平行四邊形的性質得,S平行四邊形=2S△ABC=24.
點評 此題是四邊形綜合題,主要考查了三角形的面積公式,平行四邊形的性質,待定系數法;解(2)的關鍵是用面積相等建立方程,解(3)的關鍵是利用平行四邊形的對邊平行和相等求出點P坐標.


科目:初中數學 來源: 題型:解答題
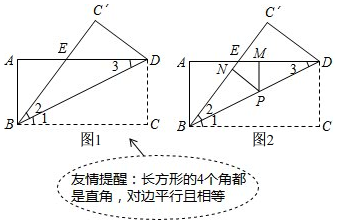
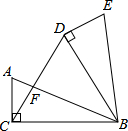 如圖所示,在△ABC=90°,AC=5cm,BC=12cm,將△ABC繞點B順時針旋轉60°,得到△BDE,連接DC交AB于點F.
如圖所示,在△ABC=90°,AC=5cm,BC=12cm,將△ABC繞點B順時針旋轉60°,得到△BDE,連接DC交AB于點F.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | a>0,△>0 | B. | a>0,△<0 | C. | a<0,△>0 | D. | a<0,△<0 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com