
分析 先解不等式2x-b>-3時,得x>$\frac{b-3}{2}$;再求出函數y=2x+b沿x軸翻折后的解析式為y=-2x+b,解不等式-2x-b>-3,得x<$\frac{b+3}{2}$;根據x滿足-4<x<0,得出$\frac{b-3}{2}$=-4,$\frac{b+3}{2}$=0,進而求出b的取值范圍.
解答 解:∵y=2x-b,
∴當y>-3時,2x-b>-3,解得x>$\frac{b-3}{2}$;
∵函數y=2x-b沿x軸翻折后的解析式為-y=2x-b,即y=-2x+b,
∴當y>-3時,-2x+b>-3,解得x<$\frac{b+3}{2}$;
∴$\frac{b-3}{2}$$<x<\frac{b+3}{2}$,
∵x滿足-4<x<0,
∴$\frac{b-3}{2}$=-4,$\frac{b+3}{2}$=0,
∴b=-5,b=-3,
∴b的取值范圍為-5≤b≤-3.
故答案為-5≤b≤-3.
點評 本題考查了一次函數圖象與幾何變換,求出函數y=2x-b沿x軸翻折后的解析式是解題的關鍵.


科目:初中數學 來源: 題型:解答題
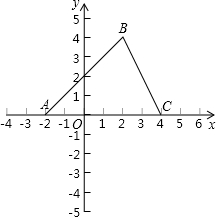 如圖,在直角坐標系中,△ABC的頂點A(-2,0),B(2,4),C(4,0).
如圖,在直角坐標系中,△ABC的頂點A(-2,0),B(2,4),C(4,0).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ∠A+∠B=180° | B. | ∠B+∠D=180° | C. | ∠B+∠C=180° | D. | ∠A+∠B=180° |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,OA⊥OC,OB⊥OD,四位同學分別說了自己的觀點.甲:∠AOB=∠COD,乙:∠BOC+∠AOD=180°,丙:∠AOB與∠COD都是∠BOC的余角,丁:圖中小于平角的角有4個,其中正確的結論有( )
如圖,OA⊥OC,OB⊥OD,四位同學分別說了自己的觀點.甲:∠AOB=∠COD,乙:∠BOC+∠AOD=180°,丙:∠AOB與∠COD都是∠BOC的余角,丁:圖中小于平角的角有4個,其中正確的結論有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (a+b)(b-a)=a2-b2 | B. | (a-b)2=a2-b2 | ||
| C. | (2x-y)2=4x2-2xy+y2 | D. | (x-2y)(-2y-x)=4y2-x2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com