
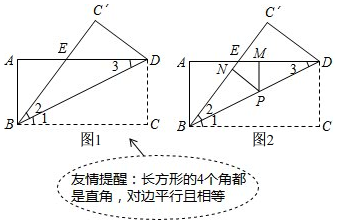
分析 (1)由折疊和平行線性質(zhì)可得:∠3=∠2,根據(jù)等角對等邊得BE=DE,所以△BDE是等腰三角形;
(2)設DE=x,則AE=8-x,BE=x,根據(jù)勾股定理列方程可求得AE的長;
(3)先判斷出PH⊥BC,再用角平分線定理得出PN=PH,即可得出結(jié)論.
解答 解:(1)由翻折知,∠1=∠2,
∵AD∥BC,
∴∠3=∠2,
∴∠1=∠3,
∴BE=DE,
即△BED是等腰三角形;
(2)設DE=x,則AE=8-x,BE=x,
在Rt△ABE中,x2=(8-x)2+42,
解之,x=5,
∴DE=5;
(3)PM+PN為定值,是4,
如圖,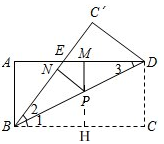
延長MP,交BC于點H,
∵AD∥BC,PM⊥AD,
∴PH⊥BC,
∵∠1=∠2,PN⊥BE,PH⊥BC,
∴PN=PH,
∴PM+PN=MN=AB=4.
點評 此題是四邊形綜合題,主要考查了矩形、折疊的性質(zhì)及等腰三角形的判定、勾股定理,角平分線定理,在四邊形計算中,常利用勾股定理列方程求邊的長度.


科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
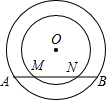 如圖,同心⊙O中,大圓弦AB與小圓交于點M、N.
如圖,同心⊙O中,大圓弦AB與小圓交于點M、N.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
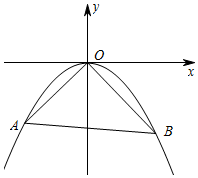 如圖,直線y=kx+b(b<0)與拋物線y=ax2相交于點A(x1,y1),B(x2,y2)兩點,拋物線y=ax2經(jīng)過點(4,-2)
如圖,直線y=kx+b(b<0)與拋物線y=ax2相交于點A(x1,y1),B(x2,y2)兩點,拋物線y=ax2經(jīng)過點(4,-2)查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
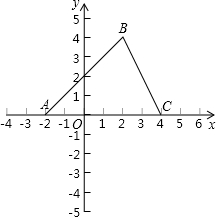 如圖,在直角坐標系中,△ABC的頂點A(-2,0),B(2,4),C(4,0).
如圖,在直角坐標系中,△ABC的頂點A(-2,0),B(2,4),C(4,0).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com