
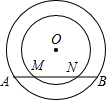
 如圖,同心⊙O中,大圓弦AB與小圓交于點M、N.
如圖,同心⊙O中,大圓弦AB與小圓交于點M、N.分析 (1)過O作OE⊥AB,根據垂徑定理得到AE=BE,ME=NE,從而得到AM=BN;
(2)由(1)可知,OE⊥AB且OE⊥NM,連接OM,OA,再根據勾股定理求出OE及OM的長即可.
解答 解:(1)如圖1所示:過點E作OE⊥AB,垂足為E.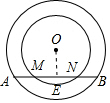
圖1
∵OA⊥AB,
∴AE=BE,ME=NE.
∴AE-ME=EB-NE,即AM=NB.
(2)如圖2所示: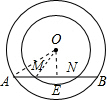
圖2
∵AE=BE,AB=8,
∴AE=4.
又∵AO=5,
∴OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=3.
∵ME=NE,MN=4,
∴ME=2.
∴OM=$\sqrt{O{E}^{2}+M{E}^{2}}$=$\sqrt{13}$.
點評 本題考查的是垂徑定理,根據題意作出輔助線,構造出直角三角形是解答此題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com