
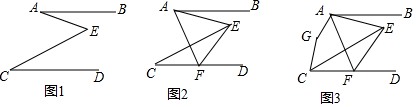
分析 (1)過(guò)E作EF∥AB,根據(jù)平行線的性質(zhì),即可得出∠A=∠AEF,∠C=∠CEF,進(jìn)而得到∠AEC=∠AEF+∠CEF=∠A+∠C;
(2)設(shè)∠BAE=α,∠DCE=β,由(1)可得,∠AEC=∠BAE+∠C=α+β,根據(jù)角的和差關(guān)系可得,∠BAF=∠EAF+∠BAE=α+2β+α=2(α+β),最后根據(jù)∠AFC=∠BAF=2(α+β),可得∠AFC=2∠AEC;
(3)設(shè)∠G=α,根據(jù)5∠AFC=2∠G,可得∠AFC=$\frac{2}{5}$α,再根據(jù)∠AFC=2∠AEC,可得∠AEC=$\frac{1}{2}$∠AFC=$\frac{1}{5}$α,最后根據(jù)四邊形AECG中,∠GCE與∠GAE互為補(bǔ)角,可得∠G+∠AEC=180°,據(jù)此可得方程α+$\frac{1}{5}$α=180°,求得∠G的度數(shù)為150°.
解答 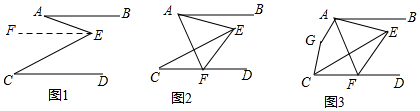 解:(1)如圖,過(guò)E作EF∥AB,
解:(1)如圖,過(guò)E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥CD,
∴∠A=∠AEF,∠C=∠CEF,
∴∠AEC=∠AEF+∠CEF=∠A+∠C;
(2)設(shè)∠BAE=α,∠DCE=β,則
由(1)可得,∠AEC=∠BAE+∠C=α+β,
∵∠EFD=2∠C,∠EFD=∠C+∠CEF,
∴∠C=∠CEF=β,
∴∠AEF=α+2β,
又∵∠FAE=∠FEA,
∴∠FAE=α+2β,
∴∠BAF=∠EAF+∠BAE=α+2β+α=2(α+β),
又∵AB∥CD,
∴∠AFC=∠BAF=2(α+β),
∴∠AFC=2∠AEC;
(3)設(shè)∠G=α,
根據(jù)5∠AFC=2∠G,可得∠AFC=$\frac{2}{5}$α,
又∵∠AFC=2∠AEC,
∴∠AEC=$\frac{1}{2}$∠AFC=$\frac{1}{5}$α,
∵四邊形AECG中,∠GCE與∠GAE互為補(bǔ)角,
∴∠G+∠AEC=180°,
即α+$\frac{1}{5}$α=180°,
∴α=150°,
即∠G的度數(shù)為150°.
點(diǎn)評(píng) 本題主要考查了平行線的性質(zhì),三角形內(nèi)角和定理以及四邊形內(nèi)角和的綜合應(yīng)用,解決問(wèn)題的關(guān)鍵是掌握:兩直線平行,內(nèi)錯(cuò)角相等.解題時(shí)注意方程思想的運(yùn)用.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,有一條小路穿過(guò)長(zhǎng)方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,則這條小路AECF的面積是多少?
如圖,有一條小路穿過(guò)長(zhǎng)方形的草地ABCD,若AB=60m,BC=84m,AE=100m,AE∥CF,則這條小路AECF的面積是多少?查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
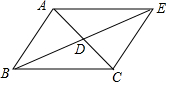 如圖所示,延長(zhǎng)△ABC的中線BD至點(diǎn)E,使DE=BD,連結(jié)AE、CE.
如圖所示,延長(zhǎng)△ABC的中線BD至點(diǎn)E,使DE=BD,連結(jié)AE、CE.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
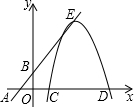 如圖,一次函數(shù)y=x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,一拋物線的頂點(diǎn)在直線AB上,形狀與函數(shù)y=-$\frac{1}{2}$x2圖象相同,它與x軸分別交于點(diǎn)C、D(點(diǎn)C在點(diǎn)D的左側(cè)),拋物線的頂點(diǎn)為點(diǎn)E.
如圖,一次函數(shù)y=x+2與x軸交于點(diǎn)A,與y軸交于點(diǎn)B,一拋物線的頂點(diǎn)在直線AB上,形狀與函數(shù)y=-$\frac{1}{2}$x2圖象相同,它與x軸分別交于點(diǎn)C、D(點(diǎn)C在點(diǎn)D的左側(cè)),拋物線的頂點(diǎn)為點(diǎn)E.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
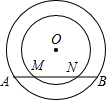 如圖,同心⊙O中,大圓弦AB與小圓交于點(diǎn)M、N.
如圖,同心⊙O中,大圓弦AB與小圓交于點(diǎn)M、N.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
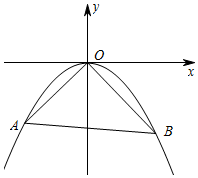 如圖,直線y=kx+b(b<0)與拋物線y=ax2相交于點(diǎn)A(x1,y1),B(x2,y2)兩點(diǎn),拋物線y=ax2經(jīng)過(guò)點(diǎn)(4,-2)
如圖,直線y=kx+b(b<0)與拋物線y=ax2相交于點(diǎn)A(x1,y1),B(x2,y2)兩點(diǎn),拋物線y=ax2經(jīng)過(guò)點(diǎn)(4,-2)查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com