Question

8．如圖，直徑為AB的⊙O交Rt△BCD的兩條直角邊BC、CD于點E、F，且$\widehat{AF}$=$\widehat{EF}$，連接BF．
（1）求證：CD為⊙O的切線；
（2）當CF=1且∠D=30°時，求AD長．

Answer 1

分析 （1）連接OF，只要證明OF∥BC，即可推出OF⊥CD，由此即可解決問題．
（2）連接AF．思想在Rt△BCF中，求出BC，再在Rt△DBC中，求出DB，在Rt△ABF中，求出AB，根據(jù)AD=DB-AB即可解決問題．

解答 （1）證明：連接OF．
∵$\widehat{AF}=\widehat{EF}$，
∴∠CBF=∠FBA，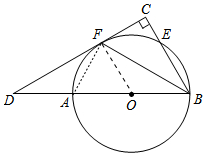
∵OF=OB，
∴∠FBO=∠OFB，
∴∠CBF=∠OFB，
∴BC∥OF，
∴∠OFC+∠C=180°，
∵∠C=90°，
∴∠OFC=90°，即OF⊥DC，
∴CD為⊙O的切線．

（2）解：連接AF．
∵∠D=30°，∠C=90°，
∴∠CBD=60°
∵$\widehat{AF}=\widehat{EF}$，
∴∠CBF=∠DBF=$\frac{1}{2}$∠CBD=30°，
在Rt△BCF中，∵FC=1，∠CBF=30°，
∴BF=2CF=2．
∴BC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∵AB是⊙O的直徑，
∴∠AFB=90°，
在Rt△AFB中，∵∠ABF=30°，BF=2，
∴AF=$\frac{1}{2}$AB．
∴AB²=（$\frac{1}{2}$AB）²+BF²，即$\frac{3}{4}$AB²=4，AB=$\frac{4\sqrt{3}}{3}$，
在Rt△DCB中，∵∠D=30°，BC=$\sqrt{3}$，
∴BD=2BC=2$\sqrt{3}$．
∴AD=DB-AB=2$\sqrt{3}$-$\frac{{4\sqrt{3}}}{3}$=$\frac{{2\sqrt{3}}}{3}$．

點評 本題考查切線的判定、直角三角形30度角的性質(zhì)、勾股定理等知識，解題的關(guān)鍵是靈活運用所學知識解決問題，學會添加常用輔助線，構(gòu)造直角三角形解決問題，屬于中考常考題型．