
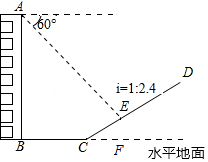
 如圖,一樓房AB后有一小山坡,其坡度為i=1:2.4,山坡坡面上E點處有一亭子,測得山坡腳C與樓房水平距離BC=30米,與亭子距離CE=26米,小麗從樓房頂測得E點的俯角為60°,求樓房AB的高.
如圖,一樓房AB后有一小山坡,其坡度為i=1:2.4,山坡坡面上E點處有一亭子,測得山坡腳C與樓房水平距離BC=30米,與亭子距離CE=26米,小麗從樓房頂測得E點的俯角為60°,求樓房AB的高.分析 過點E作EF⊥BC的延長線于點F,作EH⊥AB于點H,根據坡度的概念求出EF、CH,根據正切的定義求出AH,計算即可.
解答 解:過點E作EF⊥BC的延長線于點F,作EH⊥AB于點H,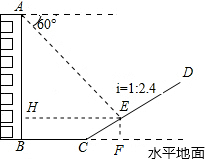
在Rt△CEF中,∵i=CF:EF=$\frac{5}{12}$,CE=26米,
∴EF=10米,CF=24米,
∴BH=EF=10米,HE=BF=BC+CF=54米,
在Rt△AHE中,∵∠HAE=30°,
∴AH=$\frac{EH}{tan30°}$=54$\sqrt{3}$米,
∴AB=AH+HB=(10+54$\sqrt{3}$)米.
答:樓房AB的高為(10+54$\sqrt{3}$)米.
點評 本題考查的是解直角三角形的應用-坡度坡角問題,掌握坡度坡角的概念、熟記銳角三角函數的定義是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
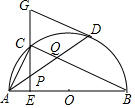 如圖,在⊙O中,AB是直徑,點D是⊙O上一點,點C是弧AD的中點,弦CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC,給出下列結論:①∠DAC=∠ABC;②AD=CB;③點P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正確的結論是( )
如圖,在⊙O中,AB是直徑,點D是⊙O上一點,點C是弧AD的中點,弦CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC,給出下列結論:①∠DAC=∠ABC;②AD=CB;③點P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正確的結論是( )| A. | ①③⑤ | B. | ②④⑤ | C. | ①②⑤ | D. | ①③④ |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 三角形的兩條平分線的交點 | |
| B. | 三角形的兩條高的交點 | |
| C. | 三角形的三條中線的交點 | |
| D. | 三角形的三條邊的垂直平分線的交點 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
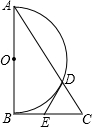 如圖,Rt△ABC中,∠ABC=90°,以AB的中點O為圓心、OA長為半徑作半圓,交AC于點D,點E為BC的中點,連接DE.
如圖,Rt△ABC中,∠ABC=90°,以AB的中點O為圓心、OA長為半徑作半圓,交AC于點D,點E為BC的中點,連接DE.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖是三個反比例函數y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x軸上方的圖象,由此觀察得到k1、k2、k3的大小關系為( )
如圖是三個反比例函數y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x軸上方的圖象,由此觀察得到k1、k2、k3的大小關系為( )| A. | k1>k2>k3 | B. | k2>k1>k3 | C. | k3>k2>k1 | D. | k3>k1>k2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com