
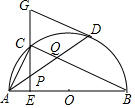
 如圖,在⊙O中,AB是直徑,點D是⊙O上一點,點C是弧AD的中點,弦CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC,給出下列結(jié)論:①∠DAC=∠ABC;②AD=CB;③點P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正確的結(jié)論是( )
如圖,在⊙O中,AB是直徑,點D是⊙O上一點,點C是弧AD的中點,弦CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC,給出下列結(jié)論:①∠DAC=∠ABC;②AD=CB;③點P是△ACQ的外心;④AC2=AE•AB;⑤CB∥GD,其中正確的結(jié)論是( )| A. | ①③⑤ | B. | ②④⑤ | C. | ①②⑤ | D. | ①③④ |
分析 在同圓或等圓中,同弧或等弧所對的圓周角相等,據(jù)此推理可得①正確,②錯誤;通過推理可得∠ACE=∠CAP,得出AP=CP,再根據(jù)∠PCQ=∠PQC,可得出PC=PQ,進而得到AP=PQ,即P為Rt△ACQ斜邊AQ的中點,故P為Rt△ACQ的外心,即可得出③正確;連接BD,則∠ADG=∠ABD,根據(jù)∠ADG≠∠BAC,∠BAC=∠BCE=∠PQC,可得出∠ADG≠∠PQC,進而得到CB與GD不平行,可得⑤錯誤.
解答  解:∵在⊙O中,點C是$\widehat{AD}$的中點,
解:∵在⊙O中,點C是$\widehat{AD}$的中點,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠CAD=∠ABC,故①正確;
∵$\widehat{AC}$≠$\widehat{BD}$,
∴$\widehat{AD}$≠$\widehat{BC}$,
∴AD≠BC,故②錯誤;
∵AB是⊙O的直徑,
∴∠ACB=90°,
又∵CE⊥AB,
∴∠ACE+∠CAE=∠ABC+∠CAE=90°,
∴∠ACE=∠ABC,
又∵C為$\widehat{AD}$的中點,
∴$\widehat{AC}$=$\widehat{CD}$,
∴∠CAP=∠ABC,
∴∠ACE=∠CAP,
∴AP=CP,
∵∠ACQ=90°,
∴∠ACP+∠PCQ=∠CAP+∠PQC=90°,
∴∠PCQ=∠PQC,
∴PC=PQ,
∴AP=PQ,即P為Rt△ACQ斜邊AQ的中點,
∴P為Rt△ACQ的外心,故③正確;
∵AB是⊙O的直徑,
∴∠ACB=90°,
又∵CE⊥AB
∴根據(jù)射影定理,可得AC2=AE•AB,故④正確;
如圖,連接BD,則∠ADG=∠ABD,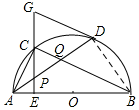
∵$\widehat{AC}$≠$\widehat{BD}$,
∴$\widehat{AD}$≠$\widehat{BC}$,
∴∠ABD≠∠BAC,
∴∠ADG≠∠BAC,
又∵∠BAC=∠BCE=∠PQC,
∴∠ADG≠∠PQC,
∴CB與GD不平行,故⑤錯誤.
故答案為:D.
點評 此題主要考查了切線的性質(zhì),圓周角定理,射影定理,圓心角、弧、弦的關(guān)系,相似三角形的判定與性質(zhì)以及三角形的外接圓與圓心的綜合應(yīng)用,熟練掌握性質(zhì)及定理是解決本題的關(guān)鍵.解題時注意:弦切角等于弦所對的圓周角.


科目:初中數(shù)學 來源: 題型:選擇題
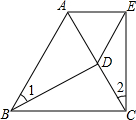 如圖,D是等邊三角形ABC的邊AC上一點,E是等邊三角形ABC外一點,若BD=CE,∠1=∠2,則△ADE的形狀是( )
如圖,D是等邊三角形ABC的邊AC上一點,E是等邊三角形ABC外一點,若BD=CE,∠1=∠2,則△ADE的形狀是( )| A. | 等腰三角形 | B. | 等邊三角形 | C. | 直角三角形 | D. | 不等邊三角形 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
 如圖,在反比例函數(shù)y=$\frac{4}{x}$(x>0)的圖象上,有點P1,P2,P3,P4…Pn(n為正整數(shù),且n≥1).它們的橫坐標依次為1,2,3,4…n(n為正整數(shù),且n≥1),分別過這些點作x軸與y軸的垂線,連接相鄰兩點,圖中所構(gòu)成的陰影部分的面積從左到右依次為S1,S2,S3…Sn-1(n為正整數(shù),且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.
如圖,在反比例函數(shù)y=$\frac{4}{x}$(x>0)的圖象上,有點P1,P2,P3,P4…Pn(n為正整數(shù),且n≥1).它們的橫坐標依次為1,2,3,4…n(n為正整數(shù),且n≥1),分別過這些點作x軸與y軸的垂線,連接相鄰兩點,圖中所構(gòu)成的陰影部分的面積從左到右依次為S1,S2,S3…Sn-1(n為正整數(shù),且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
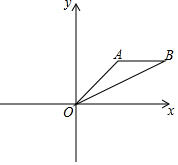 如圖,△ABO中,點O是坐標原點,A(2,2),B(4,2),點C在x軸正半軸上,O,B,C三點所構(gòu)成的三角形與△ABO相似,則點C的坐標是(2,0)或(10,0).
如圖,△ABO中,點O是坐標原點,A(2,2),B(4,2),點C在x軸正半軸上,O,B,C三點所構(gòu)成的三角形與△ABO相似,則點C的坐標是(2,0)或(10,0).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
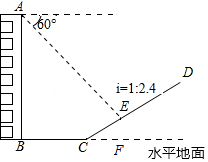 如圖,一樓房AB后有一小山坡,其坡度為i=1:2.4,山坡坡面上E點處有一亭子,測得山坡腳C與樓房水平距離BC=30米,與亭子距離CE=26米,小麗從樓房頂測得E點的俯角為60°,求樓房AB的高.
如圖,一樓房AB后有一小山坡,其坡度為i=1:2.4,山坡坡面上E點處有一亭子,測得山坡腳C與樓房水平距離BC=30米,與亭子距離CE=26米,小麗從樓房頂測得E點的俯角為60°,求樓房AB的高.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com