
分析 要求分式的分母比較大,通分會很麻煩.可通過a+b+c+d=100,變形等式里的分式,$\frac{a}{b+c+d}=\frac{100-(b+c+d)}{b+c+d}$=$\frac{100}{b+c+d}-1$,利用整體代入的方法.
解答 解:因為a+b+c+d=100,
所以$\frac{a}{b+c+d}$+$\frac{b}{a+c+d}$+$\frac{c}{a+b+d}$+$\fracp9vv5xb5{a+b+c}$=95可變形為
$\frac{100-(b+c+d)}{b+c+d}$+$\frac{100-(a+c+d)}{a+c+d}$+$\frac{100-(a+b+d)}{a+b+d}$+$\frac{100-(a+b+c)}{a+b+c}$=95
即$\frac{100}{b+c+d}-1$+$\frac{100}{a+c+d}$-1+$\frac{100}{a+b+d}-1$+$\frac{100}{a+b+c}$-1=95
所以$\frac{100}{b+c+d}$+$\frac{100}{a+c+d}$+$\frac{100}{a+b+d}$+$\frac{100}{a+b+c}$=95
所以$\frac{1}{b+c+d}+\frac{1}{a+c+d}+\frac{1}{a+b+d}+\frac{1}{a+b+c}=\frac{49}{50}$
故答案為:$\frac{49}{50}$
點評 本題考查了分式的加減,等式的變形及分式除法的相關知識.利用a+b+c+d=100,變形$\frac{a}{b+c+d}$+$\frac{b}{a+c+d}$+$\frac{c}{a+b+d}$+$\fracp9vv5xb5{a+b+c}$=95是解決本題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 2016 | B. | -2017 | C. | -2016 | D. | 2017 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1-x是一次單項式 | B. | 單項式a的系數和次數都是1 | ||
| C. | 2m-(2m+n)的運算結果為4m-n | D. | 單項式2×104x2的系數是2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,△ABC的頂點都是正方形網格中的格點,則tan∠ABC等于( )
如圖,△ABC的頂點都是正方形網格中的格點,則tan∠ABC等于( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
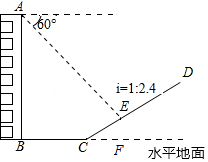 如圖,一樓房AB后有一小山坡,其坡度為i=1:2.4,山坡坡面上E點處有一亭子,測得山坡腳C與樓房水平距離BC=30米,與亭子距離CE=26米,小麗從樓房頂測得E點的俯角為60°,求樓房AB的高.
如圖,一樓房AB后有一小山坡,其坡度為i=1:2.4,山坡坡面上E點處有一亭子,測得山坡腳C與樓房水平距離BC=30米,與亭子距離CE=26米,小麗從樓房頂測得E點的俯角為60°,求樓房AB的高.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com