Question

5．（1）請寫出“直角三角形斜邊上的中線等于斜邊的一半”的逆命題，判斷這一逆命題是真命題還是假命題，如果是真命題給出證明，如果是假命題，說明理由．
（2）若一個三角形經過它的某一定點的一條直線可把它分成兩個小等腰三角形，那么我們稱該三角形為等腰三角形的生成三角形，簡稱生成三角形．
①畫出等邊△DEF的一個生成三角形，并標出生成三角形的各個角的度數；（不用尺規作圖，畫出簡圖即可）
②若等腰△ABC有一個內角等于36°，那么請你畫出簡圖說明△ABC是生成三角形．（要求畫出直線，標注出圖中等腰三角形的頂角、底角的度數）

Answer 1

分析 （1）先寫出“直角三角形斜邊上的中線等于斜邊的一半”的逆命題，再根據等腰三角形的性質得出∠A=∠ACD，∠BCD=∠B，根據三角形的內角和定理得出∠BCD+∠B+∠A+∠ACD=180°，代入即可求出∠BCD+∠ACD=90°，即∠ACB=90°，即可推出答案；
（2）①延長△DEF的邊EF至G，使得FG=DF，連接DG，△DEG即為所求；②若等腰三角形的頂角是36°，可畫底角的角平分線，可得答案；若等腰三角形的頂角是108°，把頂角分成36°和72°兩部分，可得答案．

解答 解：（1）逆命題是：如果一個三角形一邊上的中線等于這邊的一半，那么這個三角形是直角三角形．
已知，如圖，△ABC中，D是AB邊的中點，且CD=$\frac{1}{2}$AB．
求證：△ABC是直角三角形．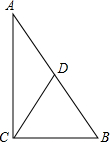

證明：∵D是AB邊的中點，且CD=$\frac{1}{2}$AB，
∴AD=BD=CD，
∵AD=CD，
∴∠ACD=∠A，
∵BD=CD，
∴∠BCD=∠B，
又∵∠ACD+∠BCD+∠A+∠B=180°，
∴2（∠ACD+∠BCD）=180°，
∴∠ACD+∠BCD=90°，
∴∠ACB=90°，
∴△ABC是直角三角形．

（2）①如圖所示，△DEG即為所求，其中∠E=60°，∠G=30°，∠EDG=90°；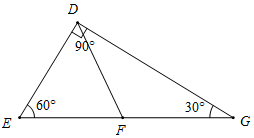

②如圖所示，等腰△ABC是生成三角形．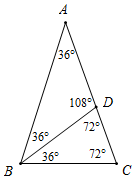

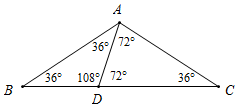
點評 本題屬于三角形綜合題，主要考查了等腰三角形的判定與性質以及三角形的內角和定理的運用．解題時注意：等角對等邊是判定等腰三角形的方法；三角形內角和是180°．