Question

20．如圖，正方形ABCD中，點E，F，G分別為邊AB，BC，AD上的點，且AE=BF=DG，連接EF，GE，GF．
（1）△BEF可以看成是△AGE繞點M逆時針旋轉α角所得，請在圖中畫出點M，并直接寫出α角的度數；
（2）當點E位于何處時，△EFG的面積取得最小值，請說明理由．

Answer 1

分析 （1）連接BD交GF于點M即可，根據題意確定旋轉角；
（2）設正方形邊長為a，AE=BF=DG=x，證明Rt△GAE和Rt△EBF，得到∠GEF是等腰直角三角形，根據三角形的面積公式列出二次函數解析式，根據二次函數的性質得到答案．

解答 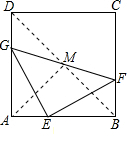解：（1）如圖，連接BD交GF于點M，則點M即為所求，
旋轉α=∠AMB=90°；
（2）當點E位于AB的中點時，△EFG面積取得最小值．
理由如下：設正方形邊長為a，AE=BF=DG=x，
則AG=a-x，
在Rt△GAE中，GE²=AG²+AE²=（a-x）²+x²=2x²-2ax+a²，
在Rt△GAE和Rt△EBF中，
$\left\{\begin{array}{l}{GA=EB}\\{∠DAB=∠ABC}\\{AE=BF}\end{array}\right.$，
∴Rt△GAE和Rt△EBF，
∴GE=FE，∠AEG=∠BFE，
∴∠GEF是等腰直角三角形，
∴△EFG的面積=$\frac{1}{2}$GE²=（x-$\frac{1}{2}$a）²+$\frac{1}{4}$a²，
所以當x=$\frac{1}{2}$a，即點E位于AB的中點時，△EFG面積取得最小值；

點評 本題考查的是正方形的性質、旋轉的性質以及二次函數的性質，正確根據題意列出二次函數解析式是解題的關鍵．