Question

15．如圖，在Rt△ABC中，點(diǎn)D在BC上，∠ADC=45°，DC=6，sinB=$\frac{3}{5}$，求∠BAD的正切值．

Answer 1

分析 由已知∠ADC=45°，DC=6，可求出CD、AD的長(zhǎng)，由sinB=$\frac{3}{5}$，AC=6，可求出AB、BC、CD的長(zhǎng)．要求∠BAD的正切值，需構(gòu)造直角三角形，過(guò)點(diǎn)D作DE⊥AB，求AE、DE的長(zhǎng)是關(guān)鍵，在Rt△BDE中，由sinB、BD求出DE、BE的長(zhǎng)．

解答 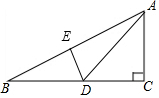解：過(guò)點(diǎn)D作DE⊥AB，垂足為E．
Rt△ADC中，∵∠ADC=45°，AC=6，
∴CD=6，AD=6$\sqrt{2}$．
在Rt△ABC中，∵AC=6，sinB=$\frac{3}{5}$，
∴AB=$\frac{AC}{sinB}=\frac{6}{\frac{3}{5}}=10$，
由勾股定理，得BC=$\sqrt{1{0}^{2}-{6}^{2}}$=8．
∴BD=BC-CD=8-6=2．
在Rt△BDE中，DE=sinB×BD=$\frac{3}{5}$×2=$\frac{6}{5}$．
在Rt△ADE中，AE=$\sqrt{A{D}^{2}-D{E}^{2}}$
=$\sqrt{（{6\sqrt{2}）}^{2}-（\frac{6}{5}）^{2}}$
=$\frac{42}{5}$
∴tan∠BAD=$\frac{DE}{AE}$
=$\frac{6}{5}×\frac{5}{42}$
=$\frac{1}{7}$．

點(diǎn)評(píng) 本題主要考查了銳角三角函數(shù)、勾股定理等相關(guān)知識(shí)．由題目要求構(gòu)造直角三角形、熟練掌握銳角三角函數(shù)的邊角關(guān)系及勾股定理是解決本題的關(guān)鍵．