
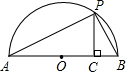
 已知a、b是正實數,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.
已知a、b是正實數,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.分析 (1)已知不等式左邊利用完全平方公式化簡,整理即可得證;
(2)連接OP,利用直徑所對的圓周角為直角且PC與AB垂直,得到三角形APC與三角形PBC相似,由相似得比例表示出PC,根據垂線段最短即可得證.
解答 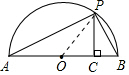 解:(1)由($\sqrt{a}-\sqrt{b}$)2≥0,得到a-2$\sqrt{ab}$+b≥0,
解:(1)由($\sqrt{a}-\sqrt{b}$)2≥0,得到a-2$\sqrt{ab}$+b≥0,
于是a+b≥2$\sqrt{ab}$,
則$\frac{a+b}{2}$≥$\sqrt{ab}$;
(2)連接OP,
∵AB為直徑,
∴∠APB=90°,
∵PC⊥AB,
∴Rt△APC∽Rt△PBC,
∴$\frac{PC}{AC}$=$\frac{CB}{PC}$,即PC2=AC•CB=ab,
∴PC=$\sqrt{ab}$,
∵PO=$\frac{a+b}{2}$,
由垂線段最短得到PO≥PC,
則$\frac{a+b}{2}$≥$\sqrt{ab}$.
點評 此題考查了相似三角形的判定與性質,圓周角定理,以及垂徑定理,熟練掌握相似三角形的判定與性質是解本題的關鍵.


 應用題作業本系列答案
應用題作業本系列答案科目:初中數學 來源: 題型:填空題
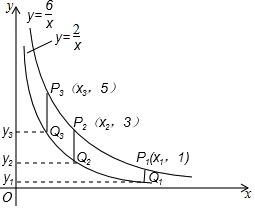 兩個反比例函數y=$\frac{2}{x}$,y=$\frac{6}{x}$在第一象限內的圖象如圖所示,點P1,P2,P3…,P2017在反比例函數y=$\frac{6}{x}$圖象上,它們的橫坐標分別是x1,x2,x3…,x2017,縱坐標分別是1,3,5,…,共2017個連續奇數,過點P1,P2,P3,…P2017分別作y軸的平行線,與y=$\frac{2}{x}$的圖象交點依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2017(x2017,y2017),則y2017=$\frac{4033}{3}$.
兩個反比例函數y=$\frac{2}{x}$,y=$\frac{6}{x}$在第一象限內的圖象如圖所示,點P1,P2,P3…,P2017在反比例函數y=$\frac{6}{x}$圖象上,它們的橫坐標分別是x1,x2,x3…,x2017,縱坐標分別是1,3,5,…,共2017個連續奇數,過點P1,P2,P3,…P2017分別作y軸的平行線,與y=$\frac{2}{x}$的圖象交點依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2017(x2017,y2017),則y2017=$\frac{4033}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 20元 | B. | 19元 | C. | 18元 | D. | 17元 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
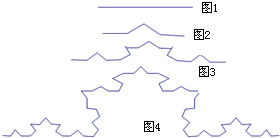 若圖1中的線段長為1,將此線段三等分,并以中間的一段為邊作等邊三角形,然后去掉這一段,得到圖2稱第1次操作,再將圖2中的每一段類似變形,得到圖3即第2次操作,按上述方法繼續得到圖4為第3次操作,則第4次操作后折線的總長度為$\frac{64}{27}$.
若圖1中的線段長為1,將此線段三等分,并以中間的一段為邊作等邊三角形,然后去掉這一段,得到圖2稱第1次操作,再將圖2中的每一段類似變形,得到圖3即第2次操作,按上述方法繼續得到圖4為第3次操作,則第4次操作后折線的總長度為$\frac{64}{27}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com