
分析 (1)將分母有理化即可;
(2)原式各項分母有理化,計算即可得到結果;
(3)原式各項分母有理化,計算即可得到結果.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}-\sqrt{n}$;
(2)($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2009}+\sqrt{2008}}$)•($\sqrt{2009}$+1)
=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2009}$-$\sqrt{2008}$)•($\sqrt{2009}$+1)
=($\sqrt{2009}$-1)•($\sqrt{2009}$+1)=2008;
(3)$\frac{1}{2\sqrt{1}+1\sqrt{2}}$+$\frac{1}{3\sqrt{2}+2\sqrt{3}}$+$\frac{1}{4\sqrt{3}+3\sqrt{4}}$+…+$\frac{1}{2009\sqrt{2008}+2008\sqrt{2009}}$=$\frac{1}{\sqrt{2}(\sqrt{2}+1)}$+$\frac{1}{\sqrt{6}(\sqrt{3}+\sqrt{2})}$+$\frac{1}{\sqrt{12}(\sqrt{4}+\sqrt{3})}$+…+$\frac{1}{\sqrt{2008×2009}(\sqrt{2009}+\sqrt{2008})}$
=$\frac{\sqrt{2}-1}{\sqrt{2}}$+$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}$+$\frac{\sqrt{4}-\sqrt{3}}{\sqrt{12}}$+…+$\frac{\sqrt{2009}-\sqrt{2008}}{\sqrt{2009×2008}}$=$\frac{\sqrt{2}-1}{\sqrt{2}×1}$+$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}×\sqrt{2}}$-$\frac{\sqrt{4}-\sqrt{3}}{\sqrt{4}×\sqrt{3}}$+…+$\frac{\sqrt{2009}-\sqrt{2008}}{\sqrt{2009}×\sqrt{2008}}$=1-$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{2}}$-$\frac{1}{\sqrt{3}}$+$\frac{1}{\sqrt{4}}$-$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2008}}$-$\frac{1}{\sqrt{2009}}$
=1-$\frac{1}{\sqrt{2009}}$=$\frac{2009-\sqrt{2009}}{2009}$.
點評 此題考查了分母有理化,正確選擇兩個二次根式,使它們的積符合平方差公式是解答問題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 6÷(-$\frac{1}{4}$)×4=6×(-4)×4 | B. | 6÷(-$\frac{1}{4}$)×4=6×(-$\frac{1}{4}$)×4 | C. | 6÷(-$\frac{1}{4}$)×4=6÷(-$\frac{1}{4}$×4) | D. | 6÷(-$\frac{1}{4}$)×4=6×(-4)÷4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 有兩個內角是60°的三角形 | |
| B. | 有兩邊相等且是軸對稱圖形的三角形 | |
| C. | 三邊都相等的三角形 | |
| D. | 有一個角是60°且是軸對稱圖形的三角形 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,∠ACB=90°,AC=BC,點D為AB中點,點E在BA的延長線上,過B作BF⊥EC交EC延長線于F,交DC延長線于G.
如圖,在△ABC中,∠ACB=90°,AC=BC,點D為AB中點,點E在BA的延長線上,過B作BF⊥EC交EC延長線于F,交DC延長線于G.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
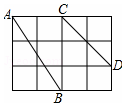 如圖,在4×3正方形網格中,每個小正方形的邊長都是1
如圖,在4×3正方形網格中,每個小正方形的邊長都是1查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (a+1)(a-1)=a2-1 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2-1=x(x-$\frac{1}{x}$) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點E,F為正方形ABCD邊BC,CD上的點,且△CEF的周長等于正方形ABCD周長的一半.
如圖,點E,F為正方形ABCD邊BC,CD上的點,且△CEF的周長等于正方形ABCD周長的一半.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com