
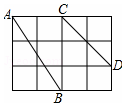
 如圖,在4×3正方形網(wǎng)格中,每個小正方形的邊長都是1
如圖,在4×3正方形網(wǎng)格中,每個小正方形的邊長都是1 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數(shù)學 來源: 題型:解答題
| 時間(秒) 路程(米) | 從比賽開始到 勻速跑前 | 從比賽開始到 勻速跑完100秒 | 從比賽開始到 勻速跑完200秒 |
| 小明 | 1600 | 1600+100a | 1600+200a |
| 小剛 | 1450 | 1450+100b | 1450+200b |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
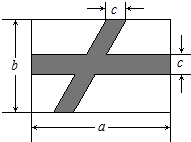 如圖所示,在公園長方形空地上,要修兩條路(圖中的陰影所示),按照圖中標的數(shù)據(jù),計算圖中空白部分的面積為( )
如圖所示,在公園長方形空地上,要修兩條路(圖中的陰影所示),按照圖中標的數(shù)據(jù),計算圖中空白部分的面積為( )| A. | ab-bc-ac+c2 | B. | bc-ab+ac | C. | b2-bc+a2-ab | D. | a2+ab+bc-ac |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com