
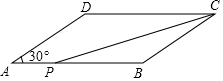
 如圖,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,點P從點A出發沿線段AB以1m/s的速度向B點移動.
如圖,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,點P從點A出發沿線段AB以1m/s的速度向B點移動.分析 (1)由等腰三角形的性質得出BP=BC=6,得出AP=AB-BP=8-6=2,求出t=2即可;
(2)由平行四邊形的性質得出AD=BC=6cm,過D作DH⊥AB于H,由含30°角的直角三角形的性質得出DH=$\frac{1}{2}$AD=3cm,求出?ABCD的面積=AB•DH=24,得出△PBC的面積=$\frac{1}{2}$BP•DH=8,求出BP=$\frac{16}{3}$cm,即可得出AP的長.
解答 解:(1)∵△PBC是等腰三角形,
∴BP=BC=6,
∴AP=AB-BP=8-6=2,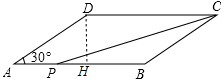
∴t=2,
即當P點運動了2秒時,△PBC為等腰三角形;
(2)∵四邊形ABCD是平行四邊形,
∴AD=BC=6cm,過D作DH⊥AB于H,
∵∠A=30°,
∴DH=$\frac{1}{2}$AD=3cm,
∴?ABCD的面積=AB•DH=8×3=24,
∴△PBC的面積=$\frac{1}{3}$×24=8=$\frac{1}{2}$BP•DH,
∴BP=$\frac{16}{3}$,
∴AP=AB-BP=8-$\frac{16}{3}$=$\frac{8}{3}$(cm).
點評 本題考查了平行四邊形的性質、等腰三角形的性質、含30°角的直角三角形的性質等知識;熟練掌握平行四邊形的性質是解決問題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$×$\sqrt{2}$=6 | B. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
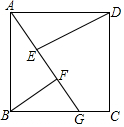 已知:如圖,四邊形ABCD是正方形,G是BC上的一點,DE⊥AG,BF⊥AG,垂足分別為E、F.
已知:如圖,四邊形ABCD是正方形,G是BC上的一點,DE⊥AG,BF⊥AG,垂足分別為E、F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y3<y2<y1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com