
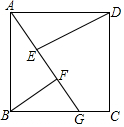
 已知:如圖,四邊形ABCD是正方形,G是BC上的一點,DE⊥AG,BF⊥AG,垂足分別為E、F.
已知:如圖,四邊形ABCD是正方形,G是BC上的一點,DE⊥AG,BF⊥AG,垂足分別為E、F.分析 (1)根據正方形的性質可得AB=AD,根據同角的余角相等求出∠BAF=∠ADE,然后利用“角角邊”證明即可;
(2)根據全等三角形對應邊相等可得AF=DE,FB=AE,然后根據AF=EF+AE等量代換即可得證.
解答 證明:(1)∵四邊形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAF+∠DAE=90°,
∵DE⊥AG,BF⊥AG,
∴∠AFB=∠DEA=90°,
∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,$\left\{\begin{array}{l}{∠BAF=∠ADE}\\{∠AFB=∠DEA=90°}\\{AB=AD}\end{array}\right.$,
∴△ABF≌△DAE(AAS);
(2)∵△ABF≌△DAE,
∴AF=DE,FB=AE,
∵AF=EF+AE,
∴DE=EF+FB.
點評 本題考查了正方形的性質,全等三角形的判定與性質,熟記性質并準確確定出三角形全等的條件是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 3.14 | C. | $\sqrt{\frac{4}{9}}$ | D. | $\root{3}{{\frac{1}{27}}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
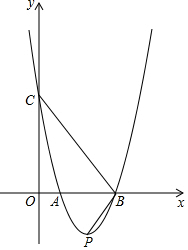 如圖,拋物線y=x2+bx+5與x軸交于點A和點B(5,0),與y軸交于點C,拋物線的頂點為點P.
如圖,拋物線y=x2+bx+5與x軸交于點A和點B(5,0),與y軸交于點C,拋物線的頂點為點P.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 數a,b在數軸上對應點A,B的位置如圖所示,且|a|=2,b是16的一個平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.
數a,b在數軸上對應點A,B的位置如圖所示,且|a|=2,b是16的一個平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
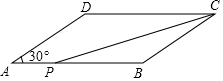 如圖,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,點P從點A出發沿線段AB以1m/s的速度向B點移動.
如圖,在?ABCD中,AB=8cm,BC=6cm,∠A=30°,點P從點A出發沿線段AB以1m/s的速度向B點移動.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
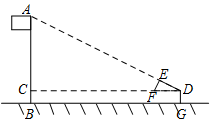 如圖,某校數學興趣小組利用自制的直角三角形硬紙板DEF來測量操場旗桿AB的高度,他們通過調整測量位置,使斜邊DF與地面保持平行并使直角邊DE與旗桿頂點A在同一直線上,已知DE=0.5米,EF=0.25米,且測點D到地面的距離DG=1.5米,到旗桿的水平距離DC=25米,求旗桿AB的高度.
如圖,某校數學興趣小組利用自制的直角三角形硬紙板DEF來測量操場旗桿AB的高度,他們通過調整測量位置,使斜邊DF與地面保持平行并使直角邊DE與旗桿頂點A在同一直線上,已知DE=0.5米,EF=0.25米,且測點D到地面的距離DG=1.5米,到旗桿的水平距離DC=25米,求旗桿AB的高度.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com