
| A. | 3-$\sqrt{6}$或1+$\sqrt{6}$ | B. | 3-$\sqrt{6}$或3+$\sqrt{6}$ | C. | 3+$\sqrt{6}$或1-$\sqrt{6}$ | D. | 1-$\sqrt{6}$或1+$\sqrt{6}$ |
分析 由解析式可知該函數在x=h時取得最小值1、x<h時,y隨x的增大而增大、當x>h時,y隨x的增大而減小,根據1≤x≤3時,函數的最小值為-5可分如下兩種情況:①若h<1≤x≤3,x=1時,y取得最小值-5;②若1≤x≤3<h,當x=3時,y取得最小值-5,分別列出關于h的方程求解即可.
解答 解:∵當x<h時,y隨x的增大而增大,當x>h時,y隨x的增大而減小,
∴①若h<1≤x≤3,x=1時,y取得最小值-5,
可得:-(1-h)2+1=-5,
解得:h=1-$\sqrt{6}$或h=1+$\sqrt{6}$(舍);
②若1≤x≤3<h,當x=3時,y取得最小值-5,
可得:-(3-h)2+1=-5,
解得:h=3+$\sqrt{6}$或h=3-$\sqrt{6}$(舍).
綜上,h的值為1-$\sqrt{6}$或3+$\sqrt{6}$,
故選:C.
點評 本題主要考查二次函數的性質和最值,根據二次函數的性質和最值分類討論是解題的關鍵.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:解答題
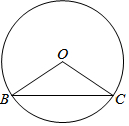 在⊙O中,己知弦BC所對的圓周角∠BAC與圓心角∠BOC互補.
在⊙O中,己知弦BC所對的圓周角∠BAC與圓心角∠BOC互補.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1cm,2cm,3.5cm | B. | 3cm,4cm,6cm | C. | 4cm,5cm,9cm | D. | 3cm,3cm,6cm |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
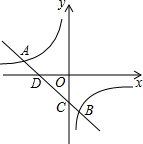 如圖,一次函數y=kx+b的圖象與反比例函數y=$\frac{m}{x}$的圖象交于A(-3,1),B(2,n)兩點,直線AB分別交x軸、y軸于D,C兩點.
如圖,一次函數y=kx+b的圖象與反比例函數y=$\frac{m}{x}$的圖象交于A(-3,1),B(2,n)兩點,直線AB分別交x軸、y軸于D,C兩點.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,正方形ABCD的邊長為1,點P為BC上任意一點(可以與B點或C重合),分別過B,C,D作射線AP的垂線,垂足分別是B',C',D',則BB'+CC'+DD'的最大值與最小值的和為2+$\sqrt{2}$.
如圖,正方形ABCD的邊長為1,點P為BC上任意一點(可以與B點或C重合),分別過B,C,D作射線AP的垂線,垂足分別是B',C',D',則BB'+CC'+DD'的最大值與最小值的和為2+$\sqrt{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
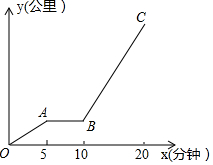 李狗蛋從家出發坐公交車去上學,他要先走到公交車站等公交車.他離家的距離y(米)與經過的時間x(分鐘)的關系折線如圖所示,已知狗蛋每分鐘能走0.1公里,公交車的速度為0.4公里/分鐘.
李狗蛋從家出發坐公交車去上學,他要先走到公交車站等公交車.他離家的距離y(米)與經過的時間x(分鐘)的關系折線如圖所示,已知狗蛋每分鐘能走0.1公里,公交車的速度為0.4公里/分鐘.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com