
 如圖,在平面直角坐標系中,四邊形ABCD是梯形,AD∥BC,E是BC的中點,BC=12,點A坐標是(0,4),CD所在直線的函數關系式為y=-x+9,點P是BC邊上一個動點,
如圖,在平面直角坐標系中,四邊形ABCD是梯形,AD∥BC,E是BC的中點,BC=12,點A坐標是(0,4),CD所在直線的函數關系式為y=-x+9,點P是BC邊上一個動點,分析 (1)由AD∥BC可知D點縱坐標為4,代入直線CD的函數關系式可求得D點坐標;
(2)由D點坐標可求得AD的長,由題意可知AD∥PE,當四邊形為平行四邊形可知AD=PE,從而可求得PE的長,則可求得BP的長.
解答 解:
(1)∵AD∥BC,且A(0,4),
∴D點縱坐標為4,
∵CD所在直線的函數關系式為y=-x+9,
∴4=-x+9,解得x=5,
∴D(5,4),
故答案為:(5,4);
(2)由(1)可知D(5,4),且A(0,4),
∴AD=5,
∵AD∥BC,
∴當以點P、A、D、E為頂點的四邊形構成平行四邊形時,AD為邊,
∴PE=AD=5,
∵E為BC中點,且BC=12,
∴BE=6,
當點P在點E左側時,則有BP=BE-PE=6-5=1,
當點P在點E右側時,則有BP=BE+PE=6+5=11,
綜上可知能構成平行四邊形,此時BP的長為1或11.
點評 本題為一次函數的綜合應用,涉及平行線的性質、平行四邊形的性質、中點及分類討論思想等知識.在(1)中確定出D點的縱坐標是解題的關鍵,在(2)中求得PE的長是解題的關鍵,注意分兩種情況.本題考查知識較基礎,難度不大.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
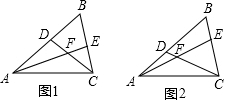
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
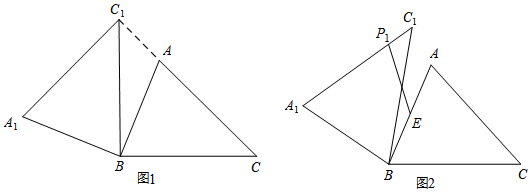
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com