
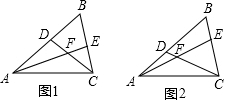
分析 (1)①由題意∠BAC+∠BCA=120°,根據(jù)∠AFC=180-∠FAC-∠FCA=180-$\frac{1}{2}(∠BAC+∠BCA)$=120°,即可解決問題.②在AC上截取AG=AD=6,連接FG.只要證明△ADF≌△AGF(SAS),推出∠AFD=∠AFG=60°,∠GFC=∠CFE=60°,再證明△CGF≌△CEF(ASA),推出CG=CE=4,由此即可解決問題.
(2)在AE上截取FH=FD,連接CH.只要證明△ADF≌△CHF(SAS),再證明CH=CE,即可解決問題.
解答 解:(1)①∵AE、CD分別為△ABC的角平分線
∴∠FAC=$\frac{1}{2}∠BAC$,∠FCA=$\frac{1}{2}∠BCA$,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180-∠FAC-∠FCA=180-$\frac{1}{2}(∠BAC+∠BCA)$=120°.
②在AC上截取AG=AD=6,連接FG.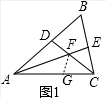
∵AE、CD分別為△ABC的角平分線
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中
$\left\{\begin{array}{l}AD=AG\\∠DAF=∠GAF\\ AF=AF\end{array}\right.$,
∴△ADF≌△AGF(SAS)
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中
$\left\{\begin{array}{l}∠GFC=∠EFC\\ CF=CF\\∠GCF=∠ECF\end{array}\right.$,
∴△CGF≌△CEF(ASA),
∴CG=CE=4,
∴AC=10.
(2)在AE上截取FH=FD,連接CH.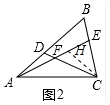
∵∠FAC=∠FCA=30°
∴FA=FC,
在△ADF和△CHF中
∵$\left\{\begin{array}{l}AF=CF\\∠AFD=∠CFH\\ DF=HF\end{array}\right.$,
∴△ADF≌△CHF(SAS),
∴AD=CH,∠DAF=∠HCF,
∵∠CEH=∠B+∠DAF=60°+∠DAF
∠CHE=∠HAC+∠HCA=60°+∠HCF
∴∠CEH=∠CHE,
∴CH=CE,
∴AD=CE.
點評 本題考查三角形綜合題、等腰三角形的判定和性質(zhì)、全等三角形的判定和性質(zhì)、角平分線的定義等知識,解題的關(guān)鍵是學(xué)會添加常用輔助線構(gòu)造全等三角形解決問題,屬于中考壓軸題.


 期末集結(jié)號系列答案
期末集結(jié)號系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
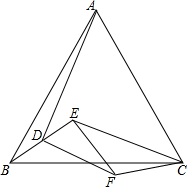 如圖,在△ABC中,AB=AC,在△EFC中,EF=FC,且∠BAC+∠EFC=180°,D是BE中點.求證:AD⊥DF.
如圖,在△ABC中,AB=AC,在△EFC中,EF=FC,且∠BAC+∠EFC=180°,D是BE中點.求證:AD⊥DF.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a>b | B. | a<b | C. | a=b | D. | 不能確定 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,在平面直角坐標(biāo)系中,四邊形ABCD是梯形,AD∥BC,E是BC的中點,BC=12,點A坐標(biāo)是(0,4),CD所在直線的函數(shù)關(guān)系式為y=-x+9,點P是BC邊上一個動點,
如圖,在平面直角坐標(biāo)系中,四邊形ABCD是梯形,AD∥BC,E是BC的中點,BC=12,點A坐標(biāo)是(0,4),CD所在直線的函數(shù)關(guān)系式為y=-x+9,點P是BC邊上一個動點,查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
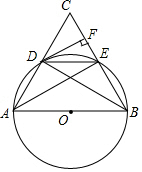 如圖,AB為⊙O的直徑,點C為圓外一點,連接AC、BC,分別與⊙O相交于點D、點E,且$\widehat{AD}$=$\widehat{DE}$,過點D作DF⊥BC于點F,連接BD、DE、AE.
如圖,AB為⊙O的直徑,點C為圓外一點,連接AC、BC,分別與⊙O相交于點D、點E,且$\widehat{AD}$=$\widehat{DE}$,過點D作DF⊥BC于點F,連接BD、DE、AE.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖是一條河,A、B是對岸兩點(AB垂直河岸),某同學(xué)站在B點,在不能到達(dá)對岸的情況下,請你幫他設(shè)計至少兩種方案求出A、B之間的距離,并請說明理由.
如圖是一條河,A、B是對岸兩點(AB垂直河岸),某同學(xué)站在B點,在不能到達(dá)對岸的情況下,請你幫他設(shè)計至少兩種方案求出A、B之間的距離,并請說明理由.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com