Question

19．[發現]如圖∠ACB=∠ADB=90°，那么點D在經過A，B，C三點的圓上（如圖①）

[思考]如圖②，如果∠ACB=∠ADB=a（a≠90°）（點C，D在AB的同側），那么點D還在經過A，B，C三點的⊙O上嗎？
我們知道，如果點D不在經過A，B，C三點的圓上，那么點D要么在⊙O外，要么在⊙O內，以下該同學的想法說明了點D不在⊙O外．請結合圖④證明點D也不在⊙O內．
【證】
[結論]綜上可得結論，如果∠ACB=∠ADB=α（點C，D在AB的同側），那么點D在經過A，B，C三點的圓上，即：A、B、C、D四點共圓．
[應用]利用上述結論解決問題：
如圖⑤，已知△ABC中，∠C=90°，將△ACB繞點A順時針旋轉α度（α為銳角）得△ADE，連接BE、CD，延長CD交BE于點F；
（1）用含α的代數式表示∠ACD的度數；
（2）求證：點B、C、A、F四點共圓；
（3）求證：點F為BE的中點．

Answer 1

分析 【思考】【證】如圖1，假設點D在⊙O內，延長AD交⊙O于點E，連接BE，則∠AEB=∠ACB，根據外角的性質得到∠ADB＞∠AEB，于是得到∠ADB＞∠ACB，于是得到結論；
【應用】（1）由題意可知，AC=AD，∠CAD=α，根據等腰三角形的性質即可得到∠ACD=90°-$\frac{1}{2}α$；
（2）根據等腰三角形的性質得到∠ABE=90°-$\frac{1}{2}$α，同時代的∠ACD=∠ABE，即可得到結論；
（3）由B、C、A、F四點共圓，得到∠BFA+∠BCA=180°，推出AF⊥BE，根據等腰三角形的性質即可得到結論．

解答 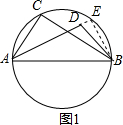【思考】【證】如圖1，假設點D在⊙O內，延長AD交⊙O于點E，連接BE，則∠AEB=∠ACB，
∵∠ADB是△BDE的外角，
∴∠ADB＞∠AEB，
∴∠ADB＞∠ACB，
因此，∠ADB＞∠ACB這與條件∠ACB=∠ADB矛盾，
∴點D也不在⊙O內，
∴點D即不在⊙O內，也不在⊙O外，點D在⊙O上；
【應用】（1）由題意可知，AC=AD，∠CAD=α，
∴∠ACD=90°-$\frac{1}{2}α$；
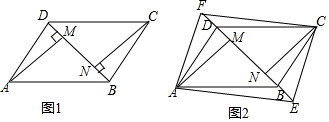
（2）∵AB=AE，∠BAE=α，∴∠ABE=90°-$\frac{1}{2}$α，∴∠ACD=∠ABE，
∴B、C、A、F四點共圓；
（3）∵B、C、A、F四點共圓，
∴∠BFA+∠BCA=180°，
又∵∠ACB=90°，
∴∠BFA=90°，
∴AF⊥BE，
∵AB=AE，
∴BF=EF，
即點F為BE的中點．

點評 本題考查的是點與圓的位置關系、圓周角定理以及反證法的應用，掌握反證法的一般步驟、同弧所對的圓周角相等是解題的關鍵．