

分析 (1)根據平行四邊形ABCD的面積=2•S△ACD,求出△ACD的面積即可.
(2)如圖2中,延長OF到M,使得FM=OF,連接CM.只要證明AC=AM,OA=AG=CE即可解決問題.
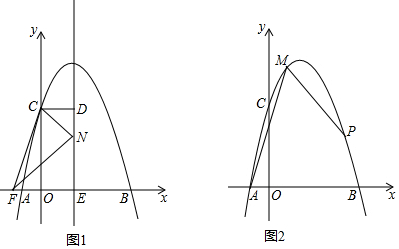
解答 解:(1)如圖1中,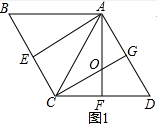
∵△ACD是等邊三角形,
∴AC=CD=AD,∠ACD=∠D=∠CAD=60°,
∵∠OAC=∠OCA=30°,
∴OA=OC=2,
∵CG平分∠ACD,
∴CG⊥AD,
在Rt∠AOG中,∵∠OAG=30°OA=2,
∴OG=$\frac{1}{2}$OA=1,AG=$\sqrt{3}$,
∴AD=2AG=2$\sqrt{3}$,
∴S△ACD=$\frac{1}{2}$•AD•CG=$\frac{1}{2}$$•2\sqrt{3}$•3=3$\sqrt{3}$.
∴平行四邊形ABCD的面積=2•S△ACD=6$\sqrt{3}$.
(2)如圖2中,延長OF到M,使得FM=OF,連接CM.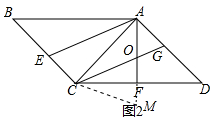
∵△ACD是等腰直角三角形,AF、CG是角平分線,
∴AF⊥CF,∠OAC=∠D=∠ACD=45°,∠OCA=∠DCG=22.5°,
∴∠COF=∠OAC+∠OCA=67.5°,∠AGC=∠D+∠GCD=67.5°,
∴∠AOG=∠AGO,
∴OA=AG,
∵CF⊥OM,OF=OM,
∴CO=CM,
∴∠M=∠COM=67.5°,
∴∠ACM=180°-∠CAM-∠M=67.5°,
∴∠CAM=∠M,
∴CA=AM,
∵∠BAE=∠GCD=22.5°,AB∥CD,
∴∠BAC=∠ACD=45°,
∴∠EAC=∠ACG=22.5°,
∴AE∥CG,∵EC∥AG,
∴四邊形AECG是平行四邊形,
∴CE=AG=OA,
∴AC=AM=OA+OM=CE+2OF.
點評 本題考查平行四邊形的判定和性質、等邊三角形的性質、等腰直角三角形的性質、等腰三角形的判定和性質、線段的垂直平分線的判定等知識,解題的關鍵是靈活運用所學知識解決問題,學會添加常用輔助線,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
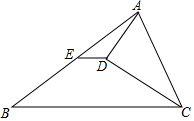 已知,如圖所示,在△ABC中,E是AB的中點,CD平分∠ACB,AD⊥CD于點D,連接ED,求證:
已知,如圖所示,在△ABC中,E是AB的中點,CD平分∠ACB,AD⊥CD于點D,連接ED,求證:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
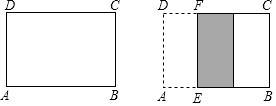 如圖,在長方形紙片ABCD中,AB=15cm,AD=10cm.將紙片沿EF折疊,EF∥AD,設AE=x(cm),折疊后重疊部分的面積為S(cm2).
如圖,在長方形紙片ABCD中,AB=15cm,AD=10cm.將紙片沿EF折疊,EF∥AD,設AE=x(cm),折疊后重疊部分的面積為S(cm2).| x/cm | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
| S/cm2 | 10 | 30 | 50 | 70 | 60 | 40 | 20 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
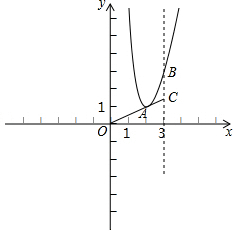 如圖,在平面直角坐標系內,拋物線y=2x2+bx+c的頂點為A(2,1),同時與直線x=3交于點B,連接OA并延長與直線x=3交于點C.
如圖,在平面直角坐標系內,拋物線y=2x2+bx+c的頂點為A(2,1),同時與直線x=3交于點B,連接OA并延長與直線x=3交于點C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com