
 如圖,點A是拋物線y=x2-4x對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為(2,-1)或(2,2).
如圖,點A是拋物線y=x2-4x對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為(2,-1)或(2,2). 分析 根據拋物線對稱軸解析式設點A坐標為(2,m),作AP⊥y軸于點P,作O′Q⊥直線x=2,證△AOP≌△AO′Q得AP=AQ=2、PO=QO′=m,則點O′坐標為(2+m,m-2),將點O′坐標代入拋物線解析式得到關于m的方程,解之可得m的值,即可得答案.
解答 解:∵拋物線y=x2-4x對稱軸為直線x=-$\frac{-4}{2}$=2,
∴設點A坐標為(2,m),
如圖,作AP⊥y軸于點P,作O′Q⊥直線x=2,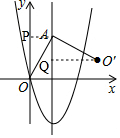
∴∠APO=∠AQO′=90°,
∴∠QAO′+∠AO′Q=90°,
∵∠QAO′+∠OAQ=90°,
∴∠AO′Q=∠OAQ,
又∠OAQ=∠AOP,
∴∠AO′Q=∠AOP,
在△AOP和△AO′Q中,
∵$\left\{\begin{array}{l}{∠APO=∠AQO′}\\{∠AOP=∠AO′Q}\\{AO=AO′}\end{array}\right.$,
∴△AOP≌△AO′Q(AAS),
∴AP=AQ=2,PO=QO′=m,
則點O′坐標為(2+m,m-2),
代入y=x2-4x得:m-2=(2+m)2-4(2+m),
解得:m=-1或m=2,
∴點A坐標為(2,-1)或(2,2),
故答案為:(2,-1)或(2,2).
點評 本題考查了坐標與圖形的變換-旋轉,全等三角形的判定與性質,函數圖形上點的特征,根據全等三角形的判定與性質得出點O′的坐標是解題的關鍵.


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:初中數學 來源: 題型:選擇題
 如圖,已知AB=CD,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )
如圖,已知AB=CD,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | MB=ND | C. | AM=CN | D. | AM∥CN |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
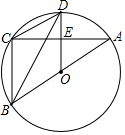 如圖,⊙O是△ABC的外接圓,AB為直徑,D是⊙O上一點,且OD⊥AC于點E,連結BD、CD.
如圖,⊙O是△ABC的外接圓,AB為直徑,D是⊙O上一點,且OD⊥AC于點E,連結BD、CD.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
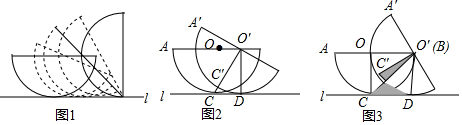 如圖1,一個半徑為2的半圓在平面作無滑動順時針滾動,可以把平面看做直線l,初始位置的半圓O與直線l相切于點C,AB∥l,滾動過程中,半圓O′與直線l相切于點D,點A、B、C在半圓O′上的對應點分別為A′、B′、C′.
如圖1,一個半徑為2的半圓在平面作無滑動順時針滾動,可以把平面看做直線l,初始位置的半圓O與直線l相切于點C,AB∥l,滾動過程中,半圓O′與直線l相切于點D,點A、B、C在半圓O′上的對應點分別為A′、B′、C′.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
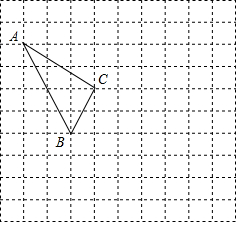 在如圖所示的正方形網格中,每個小正方形的邊長為1,格點三角形(頂點是網格線的交點的三角形)ABC的頂點A,C的坐標分別為(-4,5),(-1,3).
在如圖所示的正方形網格中,每個小正方形的邊長為1,格點三角形(頂點是網格線的交點的三角形)ABC的頂點A,C的坐標分別為(-4,5),(-1,3).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,菱形ABCD的周長為16,∠DAB=60°,對角線AC上有兩點E和F,且AE<$\frac{1}{2}$AC,AE=CF.
如圖,菱形ABCD的周長為16,∠DAB=60°,對角線AC上有兩點E和F,且AE<$\frac{1}{2}$AC,AE=CF.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com